La funzione si presenta come la somma di due funzioni, di cui una lineare e l'altra logaritmica; sappiamo che l'argomento del logaritmo deve essere un valore positivo, e poiché in questo caso l'argomento è un valore assoluto, dobbiamo escludere dal dominio della funzione solo i valori che annullano tale modulo:
Quindi abbiamo:
.
Determiniamo ora i punti di intersezione con gli assi:
Il punto individuato è
.
L'intersezione della funzione con l'asse x non può essere calcolata con metodi analitici, in quanto so dovrebbe risolvere un'equazione del tipo:
Verifichiamo se la funzione è pari o dispari:
La funzione quindi non è ne pari ne dispari.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a
:
Dalle proprietà dei valori assoluti, sappiamo che:
quando
cioè
Quindi, per l'intorno che stiamo studiando, possiamo scrivere il limite nel seguente modo:
Poiché il limite si presenta in una forma indeterminata, procediamo nel seguente modo: mettiamo in evidenza
nell'argomento del logaritmo:
Applicando le proprietà dei logaritmi si ottiene:
Ora mettiamo in evidenza
fra tutti i termini:
In questo modo possiamo calcolare il valore del limite: infatti, le frazioni che compaiono possono essere risolte facilmente, perché presentano tutte un denominatore che è un infinito di ordine maggiore del numeratore; di conseguenza, tali frazioni tendono a 0 per
.
Abbiamo quindi il risultato seguente:
La funzione, quindi, non presenta asintoti orizzontali destri.
Studiamo ora l'andamento della funzione a
.
Con un ragionamento analogo al precedente si ha:
Effettuiamo gli stessi raccoglimenti per eliminare la forma indeterminata:
La funzione, quindi, non presenta neanche asintoti orizzontali sinistri.
Non avendo asintoti orizzontali, la funzione potrebbe presentare degli asintoti obliqui; ricerchiamo, se esiste finito, il coefficiente angolare del possibile asintoto:
Scomponiamo il logaritmo fattorizzando il suo argomento e applicando le proprietà algebriche dei logaritmi:
Le frazioni presenti hanno un denominatore che è un infinito di ordine maggiore del numeratore; di conseguenza, si ha:
Poiché abbiamo ottenuto un valore finito per
, cerchiamo ora il valore di
:
Poiché
assume un valore non finito, possiamo affermare che non esistono asintoti obliqui.
Non essendo definita in
e
, studiamo il comportamento della funzione quando si avvicina a tali valori:
Possiamo scomporre il logaritmo fattorizzando il trinomio notevole che ha come argomento, e applicando poi le proprietà dei logaritmi:
Poiché si ha:
Il valore del limite sarà:
Di conseguenza, la funzione presenta un asintoto verticale di equazione
.
Vediamo ora cosa accade per
:
In questo caso:
E quindi il limite generale vale:
Abbiamo trovato che anche la retta di equazione
è asintoto verticale per la funzione.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
Troviamo i punti in cui la deriva prima si annulla:
Studiamo il segno della derivata prima:
Dallo studio del segno si ottengono i seguenti intervalli:
; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che i punti individuati da
e da
sono punti di minimo relativo per la funzione.
Calcoliamo ora la derivata seconda della funzione:
Troviamo i valori di x che annullano la derivata seconda:
Tale valore non si annulla mai, in quanto il delta è minore di zero; poiché la derivata seconda è sempre positiva, possiamo affermare che la funzione rivolge la concavità verso l'alto in tutto il suo dominio.
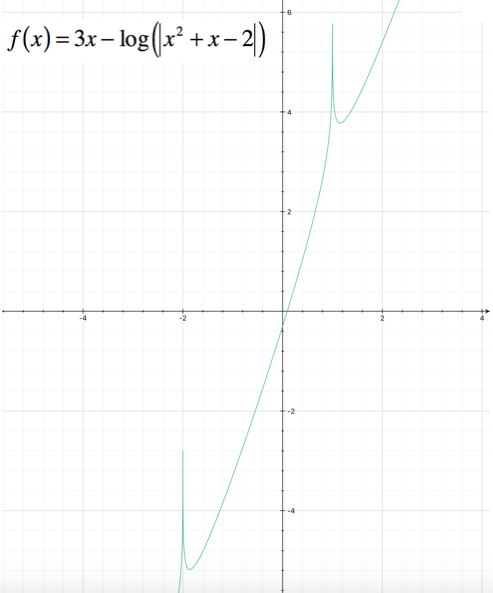
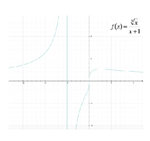
Possiamo tracciare il grafico della funzione:
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
