Equazioni di primo e secondo grado: come svolgerle e applicazioni geometriche

In quest'appunto si troverà un riassunto completo sui metodi di risoluzione delle equazioni di primo e secondo grado, arricchito dallo svolgimento commentato di un esercizio basato sulla geometria.

Cosa sono le equazioni e a cosa servono

In matematica, il concetto di uguaglianza è molto importante. Si definisce uguaglianza una quantità formata da due termini legati insieme dal simbolo uguale

. Tale quantità può contenere delle espressioni (qualora siano presenti solo numeri e operazioni) oppure delle equazioni.

La principale differenza tra un'equazione e un'espressione risiede nel ruolo dell'incognita, solitamente indicata con la lettera

. Il fine ultimo di un'equazione è, infatti, quello di scoprirne il valore. Per questo motivo, la soluzione (o radice) di un'equazione presenta la forma

.

I valori assumibili da

sono indicati dal dominio, chiamato anche insieme di definizione. L'estensione del dominio dipende dal tipo di funzioni presenti all'interno dell'equazione. Le funzioni polinomiali sono definite in

, ciò significa che la soluzione di un'incognita può assumere qualsiasi valore reale.

Le funzioni razionali, invece, devono necessariamente avere il denominatore diverso da zero: per questo motivo, qualora al denominatore della funzione sia presente l'incognita, il valore di quest'ultima dev'essere tale per cui il denominatore non debba annullarsi.
Se, infine, all'interno dell'equazione è presente una radice a indice pari cui argomento presenta un'incognita, tale argomento deve essere imposto maggiore o uguale a zero. Ciò accade perché una radice a indice pari con argomento negativo rappresenta un numero immaginario (o complesso).

Come svolgere correttamente le equazioni di primo e secondo grado

Le equazioni possono distinguersi a seconda del proprio grado. Il grado di un'equazione è il massimo esponente con cui si presenta un'incognita al suo interno. Se è presente più di un'incognita, è possibile definire un grado per ciascuna.
Un'equazione di primo grado è scrivibile nella forma

. In questo caso, per svolgere l'equazione basta applicare i due principi di equivalenza.

I principi di equivalenza sono delle regole atte a isolare l'incognita in uno dei due membri. Questo, infatti, è uno step fondamentale per la risoluzione delle equazioni di primo grado. In particolare:

• il primo principio di equivalenza afferma che sottraendo o addizionando a entrambi i membri di un'equazione la stessa quantità si ottiene una struttura equivalente
• il secondo principio di equivalenza afferma che moltiplicando e dividendo entrambi i membri per una stessa quantità, si ottiene una struttura equivalente

Nel caso dell'equazione di primo grado

, la

può essere isolata sottraendo a entrambi i membri il valore di

e dividendo entrambi per

.

La situazione si complica nel caso di equazioni di secondo grado, esprimibili nella formula

. In questo caso, la presenza del termine

impedisce la semplice applicazione dei principi di equivalenza. Bisogna, quindi, applicare una strategia risolutiva differente.

Il primo passaggio per affrontare un'equazione di secondo grado è il calcolo del discriminante

attraverso la formula

. Esso consente di conoscere a priori se le soluzioni dell'equazione siano reali e distinte

, uguali e coincidenti

o complesse coniugate

.

Dopo aver calcolato il discriminante è necessario calcolare il valore delle radici. La formula da utilizzare è la seguente:

. Anche in questo caso, il valore delle radici può essere influenzato dalla presenza del dominio.

Esercizio commentato: calcola il perimetro e l'area del trapezio isoscele sfruttando le equazioni

Nel trapezio isoscele

,

è la base maggiore e

è il piede della perpendicolare
condotta dal vertice

alla base

. Sapendo che

,

e che risulta

,
determinare

, l'area e il perimetro del trapezio.

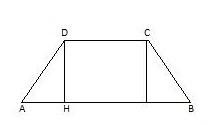
Dati del problema

Svolgimento

Poniamo

e quindi si avrà che

,

e infine per sostituzione

.

Risolviamo quindi l'equazione di primo grado

;

;

;

;

;

;

.

In conclusione

, da qui

e

.

Il trapezio è isoscele, per cui:

.

Per il Teorema di Pitagora si ha:

.

Il perimetro è dato dalla somma di tutti i lati del trapezio, cioè

.
L'area del trapezio si calcola mediante la seguente formula

.

Per ulteriori approfondimenti sulle equazioni di primo e di secondo grado vedi anche qui