Sistemi di equazioni per la risoluzione di un problema geometrico sul trapezio isoscele

In questo appunto di matematica si riporta un esempio di problema geometrico sul trapezio isoscele, la cui risoluzione richiede l’utilizzo di un sistema di equazioni di primo, a tal fine si presenta una breve introduzione sul trapezio isoscele e sui sistemi di equazioni.

Il trapezio

Definiamo trapezio un quadrangolo convesso con due lati opposti paralleli e gli altri due non paralleli.
I lati paralleli vengono chiamati basi e si distinguono in base maggiore e base minore. Gli altri due lati vengono denominati lati del trapezio o anche lati obliqui. La distanza delle rette parallele, cui appartengono le basi, si definisce altezza del trapezio.
In ogni trapezio gli angoli adiacenti a ciascuno dei lati obliqui sono supplementari, in quanto coniugati interni rispetto a due rette parallele tagliate da una trasversale.
Chiameremo trapezio isoscele, un trapezio che ha i lati obliqui uguali.
Per tale trapezio valgono, e sono di facile dimostrazione, le seguenti proprietà:

• gli angoli adiacenti a ciascuna base sono uguali;
• le diagonali sono uguali;
• le proiezioni dei lati obliqui sulla base maggiore sono uguali.

Infine, chiameremo trapezio rettangolo, un trapezio che ha un lato perpendicolare alle basi.
L’area, A, di tale quadrilatero è espressa dalla seguente formula:

dove
B è la base maggiore
b è la base minore
h è l’altezza.
Da tale formula si possono ricavare le seguenti formule inverse:

I sistemi di equazioni: definizione e proprietà

Sappiamo che un problema, sia aritmetico, sia geometrico, può coinvolgere più incognite. Tali incognite devono essere inserite all’interno di equazioni che traducono in forma matematica le condizioni espresse dal problema. Le equazioni scritte che esprimono le condizioni richieste dal problema debbono evidentemente essere verificate simultaneamente, ossia dalla medesima coppia di numeri che rappresenta la soluzione cercata: l’insieme di tali equazioni costituisce un sistema di equazioni o più brevemente un sistema.
In generale chiameremo sistema di equazioni, o semplicemente sistema, un insieme di due o più equazioni in due o più incognite (ogni equazione contiene almeno una incognita, ma non necessariamente tutte).
Definiamo soluzione di un sistema di equazioni una coppia, o una terna, ecc. ordinata di numeri, appartenenti a prefissati insiemi, che, sostituiti ciascuno alla corrispondente incognita, soddisfano simultaneamente tutte le equazioni del sistema stesso.
Sia S l’insieme delle soluzioni del sistema, si ha che:

dove

sono gli insiemi delle soluzioni delle varie equazioni.
Risolvere un sistema di equazioni significa determinare l’insieme S.
Diremo che un sistema è possibile se ammette almeno una soluzione.
Diremo che un sistema è impossibile se non ammette alcuna soluzione.
Fra i sistemi possibili si distinguono quelli determinati e quelli indeterminati a seconda che le loro soluzioni siano in numero finito o infinito.
Se tutte le equazioni che costituiscono il sistema sono razionali, definiamo grado del sistema il prodotto dei gradi delle sue equazioni.
Due sistemi che ammettono lo stesso insieme di soluzioni, si dicono equivalenti: tale relazione gode della proprietà riflessiva, simmetrica e transitiva.
In base a tali considerazioni si può asserire che vale il Criterio di Equivalenza:
se in un sistema si sostituisce una equazione con un’altra ad essa equivalente, il sistema ottenuto è equivalente al dato.

Metodi risolutivi di un sistema di equazioni

Un sistema di equazioni può essere risolto tramite uno dei tre seguenti metodi:

• metodo della sostituzione;
• metodo del confronto;
• metodo di addizione e sottrazione o riduzione.

Il Criterio di Sostituzione asserisce che: se un’espressione E figura in due equazioni di un sistema, risolvendo una equazione rispetto ad E (ossia esprimendo l’equazione nella forma E = …) e sostituendo ad E l’espressione così trovata nell’altra equazione, si ottiene un sistema equivalente al dato.
In questo modo, dato, ad esempio, un sistema di primo grado di due equazioni in due incognite, si può procedere come segue:

• si risolve una delle due equazioni rispetto ad una delle due incognite, x ad esempio, considerando l’altra incognita come una costante ed ottenendo in questo modo
  [math]
  x = f(y);
  [/math]
• si sostituisce nell’altra equazione
  [math]
  f(y)
  [/math]
  al posto della x, ottenendo una equazione nella sola incognita y;
• si risolve quest’ultima equazione rispetto all’unica incognita y, ottenendo così
  [math]
  y = y_0
  [/math]
  ;
• si trova il corrispondente valore
  [math]
  x_0
  [/math]
  di x sostituendo
  [math]
  y_0
  [/math]
  ad y nell’equazione
  [math]
  x = f(y)
  [/math]
  .

Il metodo del confronto, molto simile al metodo precedentemente esposto, consiste dei seguenti passaggi:

• si risolvono entrambe le equazioni rispetto alla medesima incognita (ad esempio x), considerando l’altra come una costante ed ottenendo in questo modo le due equazioni
  [math]
  x =f(y)
  [/math]
  ed
  [math]
  x = g(y)
  [/math]
  ;
• si uguagliano le due espressioni
  [math]
  f(y)
  [/math]
  e
  [math]
  g(y)
  [/math]
  ,
  [math]
  f(y) = g(y)
  [/math]
  , e si risolve l’equazione così ottenuta rispetto all’unica incognita y, trovando così
  [math]
  y = y_0;
  [/math]
• si determina il corrispondente valore
  [math]
  x_0
  [/math]
  di x sostituendo
  [math]
  y_0
  [/math]
  ad y in una delle due equazioni
  [math]
  x =f(y)
  [/math]
  oppure
  [math]
  x = g(y).
  [/math]

Il Criterio di addizione e sottrazione (o anche di riduzione) asserisce che: indicate con

e

due equazioni di un sistema, sostituendo una di esse con l’equazione

, ovvero con l’equazione

si ottiene un sistema equivalente a quello dato.

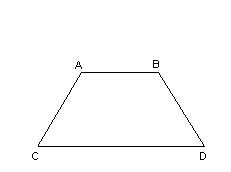
Problema geometrico risolubile con un sistema di equazioni

Si consideri un trapezio isoscele ABCD avente perimetro

. In tale trapezio la base maggiore,

, è il doppio della minore

mentre il lato obliquo

misura 13m.
Si vogliono determinare le misure delle due basi,

e

Dati

Svolgimento
Poniamo

e

Sapendo che

si ha che

e sostituendo i valori numerici si ha che:

ossia

Quindi in base ai dati forniti dal problema si può impostare un sistema di due equazioni nelle due incognite x ed y:

Per risolvere tale sistema adottiamo il metodo della sostituzione:

quindi sostituendo

nella prima equazione

e svolgendo i calcoli

da cui

quindi

sostituendo il valore della y trovato nella seconda equazione si ha che

ottenendo infine

Per cui si può concludere

per ulteriori approfondimenti sui sistemi lineari vedi anche qua