Un triangolo isoscele ha un'area di
e l'altezza relativa a uno dei suoi lati obliqui è
. Determina la base del triangolo e l'altezza relativa alla base.
Svolgimento
Prima di tutto, trasformiamo i dati tutti nella stessa unità di misura:
Chiamiamo con le incognite
e
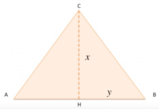
rispettivamente metà base del triangolo e l'altezza relativa alla base:
In questo caso, quindi, l'area del triangolo vale:
Possiamo trovare la misura del lato obliquo in funzione delle due incognite con i teorema di Pitagora:
Sapendo che il triangolo ha un'area di
e che l'altezza relativa a uno dei suoi lati obliqui è
, con la formula inversa dell'area possiamo ricavare il lato obliquo:
Quindi sappiamo che:
Possiamo quindi impostare il sistema:
left{ \begin{array}{rl}
frac{xy}{2} = 168 &\
sqrt{x^2 + y^2} = 25 &
end{array}\right.
[math][/math]
Ricaviamo un'incognita dalla prima equazione e risolviamo per sostituzione:
left{ \begin{array}{rl}
x = frac{336}{y} &\
sqrt{x^2 + y^2} = 25 &
end{array}\right.
[math][/math]
Sapendo che la somma di due quadrati è sempre positiva, non è necessario porre le condizioni di esistenza.
Lavoriamo sulla seconda equazione:
Calcoliamo il minimo comune multiplo all'interno della radice:
Eleviamo al quadrato:
Troviamo le soluzioni con la formula
:
Da cui si ricava:
Troviamo i corrispondenti valori di
:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
