Vediamo insieme cosa si intende quando si parla della successione di Fibonacci.
In particolare, approfondiremo i seguenti aspetti:
- Fibonacci e la sua sequenza
- La sequenza di Fibonacci: la soluzione ad un problema
- La sequenza di Fibonacci e la sezione aurea
- La sequenza di Fibonacci in natura
Indice
Fibonacci e la sua sequenza
Leonardo Pisano, figlio di Bonaccio, noto quindi anche come il Fibonacci, (1175-1235) fu un matematico italiano.
Tra le sue opere principali, a parte quelle puramente matematiche, ricordiamo il Liber Abaci, compendio matematico che non solo rivoluzionò i sistemi di numerazione, ma costituì le fondamenta per la costruzione della Ragioneria, della quale fecero uso inizialmente i mercanti toscani.
Nel Liber Abaci Fibonacci espone i fondamenti di algebra e matematica usati nei paesi Arabi; ed in particolare, un problema lì trattato fornisce l'occasione per l'introduzione della serie numerica che oggi porta il suo nome. Fibonacci introduce ancora il sistema decimale e l'uso delle cifre arabe basandosi sulle nozioni di aritmetica e di algebra che aveva accumulato durante i suoi viaggi.
Scrisse di problemi pratici di matematica finanziaria e di agrimensura, di problemi di enigmistica. I suoi indovinelli matematici, che venivano spesso presentati sotto forma di storia, divennero classici già nel XIII secolo.
Si narra che durante un torneo matematico, un problema proposto dall'imperatore Federico II di Svevia nel 1223 fu brillantemente risolto da Leonardo Pisano.
La Sequenza di Fibonacci: la soluzione ad un problema
Consideriamo il seguente problema:
La soluzione è nella Sequenza di Fibonacci. Le coppie di conigli saranno, per ogni mese:
Notiamo che ogni numero della sequenza è la somma degli altri due termini immediatamente precedenti. Questa semplice regola è l'unica regola che consente di determinare i termini della successione di Fibonacci, unita al fatto che i primi due termini della successione sono pari a
Una delle cose visivamente più famose legate alla successione di Fibonacci è la seguente:
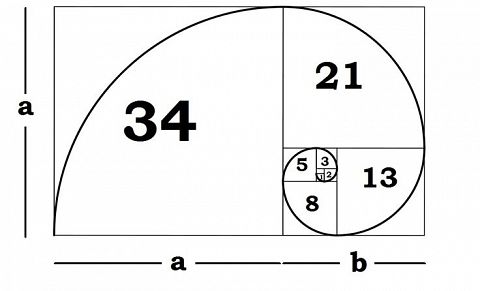
Questa figura è costruita partendo da una sequenza di quadrati, in cui ogni quadrato ha come lunghezza del lato la somma dei lati dei due quadrati dei due quadrati più vicini. Riconosciamo che le dimensioni dei quadrati, letti dal più piccolo in ordine crescente sono:
La sequenza di Fibonacci e la sezione aurea
Supponiamo di prendere un segmento e dividiamolo in due parti diseguali,
e
, in modo tale che la parte più corta,
, risulti proporzionale alla più lunga,
, allo stesso modo in cui quest'ultima è proporzionale all'intero segmento
:
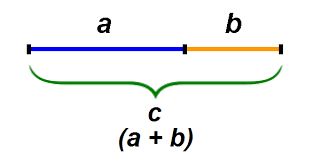
In questa proporzione così definita, il rapporto
è pari a
, cioè un numero che ha infinite cifre decimali e che rappresenta la cosiddetta sezione aurea, indicata dalla lettera
. Cos'ha di tanto particolare questo numero e qual è il suo legame con la successione di Fibonacci?
Chiamata anche "divina proporzione", la sezione aurea è un rapporto ben conosciuto sin dall'antichità ed è considerato l'elemento che caratterizza al meglio l'equilibrio di certe forme. In parole povere, esso è associato all'idea di armonia, di bellezza, come possiamo osservare in molte opere d'arte e architettoniche (una su tutte, il Partenone). Anche nel corpo umano, molte sezioni e rapporti morfologici si collegano a questo numero (ad esempio, le parti di una mano).
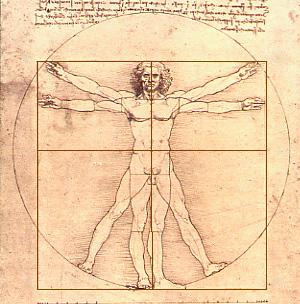
Più in generale, è la Natura stessa che sembra "amare" in modo particolare questo numero straordinario, e sembra legarlo in maniera straordinaria alla successione di Fibonacci.
È dunque arrivato il momento di svelare l'arcano: qual è il rapporto tra questa successione e la sezione aurea? Si può scoprire con facilità tramite una semplice divisione, quella fra gli elementi contigui della stessa successione, per esempio:
Il rapporto fra questi numeri, crescendo nella sequenza, si avvicina sempre più a quello della sezione aurea!
Se rivediamo l'immagine della spirale, scopriamo che il suo fattore di crescita è proprio
, la sezione aurea. Questo giustifica il suo nome di "spirale aurea".
Ecco soltanto alcuni esempi in cui la spirale aurea compare:
Scrivendo questa informazione sotto forma di limite potremo dire che:
dove
è il
-esimo numero di Fibonacci.
Per approfondimenti sui limiti, vedi anche qua.
La successione di Fibonacci in natura
Come abbiamo visto sono tantissimi i casi in cui compare la spirale aurea, a sua volta legata strettamente alla serie di Fibonacci: conchiglie, forma di piante, uragani, galassie…
Oltre a tutto ciò abbiamo ancora altre, e non saremo comunque esaustivi:
-
L'albero genealogico di un fuco:
L'albero genealogico di un fuco presenta chiaramente la sequenza di Fibonacci.
Bisogna innanzitutto dire che in uno sciame non tutte le api sono uguali: ci sono innanzitutto le api (femmine) e i fuchi (maschi).
Le femmine sono tutte generate dall'unione dell'ape regina con un fuco e si dividono in operaie e regine.
Le api regine sono api operaie nutrite con pappa reale ma, diversamente dalle operaie, sono in grado di produrre uova.
I maschi nascono dalle uova dell'ape regina.
Quindi possiamo dire che le femmine hanno 2 genitori: l'ape regina e un fuco, mentre i fuchi hanno un solo genitore: l'ape regina.
Prendiamo in esame l'albero genealogico di un fuco. 1 fuco ha 1 genitore che ha sua volta ha 2 genitori che a loro volta hanno 3 genitori che a loro volta hanno 5 genitori e così via. -
L'achillea ptarmica:
Ogni ramo impiega un mese prima di potersi biforcare.
Al primo mese quindi abbiamo 1 ramo, al secondo ne abbiamo 2, al terzo 3, al quarto 5 e così via.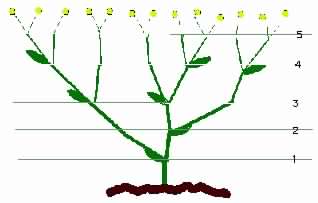
- Il girasole: L'accrescimento biologico di alcune specie, la spaziatura tra le foglie lungo uno stelo e la disposizione dei petali e dei semi in alcuni tipi di fiori come il girasole, e l'accrescimento di una pigna secondo i valori 5 e 8, sono testimonianze di sezioni auree.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
