Equazioni di secondo grado
Ogni equazione del tipo[math]ax^2+bx+c=0[/math]
dove a,b,c sono numeri reali (detti coefficienti) e a≠0, viene chiamata equazione di secondo grado (o equazione quadratica) in forma normale (o in forma canonica).Esistono 2 grandi categorie di equazioni di secondo grado: complete quando queste hanno tutti i coefficienti e incomplete quando qualcuno dei coefficienti b o c è nullo. Partiamo con l'analizzare le equazioni incomplete.
Equazioni di secondo grado incomplete
Le equazioni incomplete si dividono a loro volta in 3 tipi: monomie, pure e spurie.
Monomie
Le equazioni monomie sono quelle equazioni che hanno i coefficienti b e c = 0 ma con a ≠ 0 (altrimenti sarebbe di primo grado).Dunque, la forma di queste è:
[math]ax^2 = 0[/math]
.Le equazioni monomie hanno sempre 2 soluzioni coincidenti in cui x1 = x2 = 0. Capiamo il perchè prima col calcolo letterale poi con i numeri.
[math]ax^2 = 0 \Rightarrow x^2 = \frac{0}{a} = x^2 = 0[/math]
.Come sappiamo l'inverso di un quadrato è la radice algebrica, di conseguenza
[math]x = \pm\sqrt{0} = 0[/math]
.Ora, anche se scontato, applichiamo tutto ciò in un esempio pratico:
[math]4x^2 = 0 \Rightarrow x^2 = \frac{0}{4} = 0 \Rightarrow x = \pm\sqrt{0} = 0[/math]
.
Pure
Le equazioni pure sono quelle equazioni che hanno i coefficienti a e c ≠ 0 e b =0. La forma di queste è:[math]ax^2 + c = 0[/math]
.Ogni equazione pura può essere anzitutto risolta rispetto a x^2, così da ricondurla a un'equazione della forma:
[math]x^2 = k[/math]
con k≠0 (altrimenti sarebbe una monomia).A questo punto possiamo distinguere due casi: k0.
Se k>0 l'equazione ha 2 soluzioni reali possibili per cui il quadrato è k:
[math]\pm\sqrt{k}[/math]
. Se k
[math]ax^2 + c = 0[/math]
.Porto il termine noto a destra dell'uguale:
[math]ax^2 = -c[/math]
.Ora guardo se (-c) è > o
[math]x^2 = \frac{-c}{a} \Rightarrow x = \pm\sqrt{\frac{-c}{a}}[/math]
.Esempio pratico (senza passaggi scritti, solo svolti):
[math]x^2 - 9 = 0 \\
x^2 = 9 \Rightarrow x = \pm\sqrt{9} = \pm 3[/math]
.x^2 = 9 \Rightarrow x = \pm\sqrt{9} = \pm 3[/math]
Spurie
Le equazioni spurie sono quelle con i coefficienti a e b ≠ 0 e c = 0. Dunque sono della forma:[math]ax^2 + bx = 0[/math]
.Ogni equazione spuria può essere scomposta attraverso un raccoglimento totale della x e poi risolta con la legge di annullamento del prodotto.
Dimostrazione letterale:
[math]ax^2 + bx = 0[/math]
.Raccoglimento totale della x:
[math]x(ax+b) = 0 \\
LAP: x=0 \lor x= -\frac{b}{a}[/math]
.LAP: x=0 \lor x= -\frac{b}{a}[/math]
Dimostrazione pratica:
[math]x^2+6x=0 \\
x(x+6) = 0
LAP: x=0 \lor x=-6[/math]
.
x(x+6) = 0
LAP: x=0 \lor x=-6[/math]
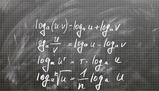
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
