Numeri complessi: Descrivere geometricamente l'insieme per cui risulta: | z^2 + 2z \bar{z} + (\bar{z})^2 | + 4 | z^2 - 2z \bar{z} + (\bar{z})^2 | <= 4

Consideriamo un generico numero complesso

della forma

; sappiamo per definizione che il suo coniugato è un numero con stessa parte reale e parte immaginaria opposta, quindi vale

.

Analizziamo, nel nostro caso, il primo modulo della disequazione, ovvero:

Notiamo, innanzitutto, che tale espressione può essere scritta come il quadrato di un binomio:

Se sostituiamo a tale espressione le considerazioni fatte in precedenza, otteniamo una forma più comprensibile dell'espressione:

Quindi, la prima espressione può essere scritta come:

, dove con

indichiamo la parte reale del numero

.

Passiamo ora al secondo modulo:

Anche in questo caso, l' espressione può essere scritta come il quadrato di un binomio:

Sostituiamo le forme generiche del numero complesso:

Questa espressione può essere scritta come:

, dove con

indichiamo la parte immaginaria del numero

.

Sostituiamo le espressioni cosi scritte alla disequazione iniziale:

Ovvero:

.

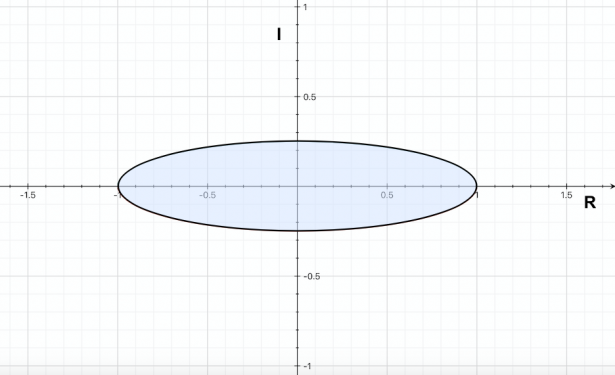
In un piano complesso la parte reale e la parte immaginaria di un numero rappresentano, rispettivamente, l'ascissa e l'ordinata del piano.
Possiamo concludere, quindi, che la disequazione rappresenta l'insieme dei punti del piano che sono racchiusi all'interno dell'ellisse di equazione

Potrebbe interessarti anche

• Numeri complessi: forma algebrica (videolezione)
• Numeri complessi (dispensa)