Procediamo considerando un generico numero complesso
[math]z[/math]
della forma [math] a + ib [/math]
; ricordando che il coniugato di un numero complesso equivale al numero complesso che ha stesa parte reale e parte immaginaria opposta, la nostra diseguaglianza diventa:
[math] ib - | a + ib + a - ib |^2 > 1 [/math]
Svolgiamo i calcoli all'interno del modulo, ed eleviamo al quadrato:
[math] b - | 2a |^2 > 1 [/math]
[math] b - 4a^2 > 1 [/math]
Portiamo tutto a primo membro, cambiamo segno alla diseguaglianza e invertiamo il verso:
[math] b - 4a^2 - 1 > 0 [/math]
[math] 4a^2 - b + 1 > 0 [/math]
Ricordiamo che nel piano complesso la parte reale del numero rappresenta l'asse orizzontale, mentre la parte immaginaria l'asse verticale; ovvero :
[math] Re(z) = a = x , Im(z) = b = y [/math]
La nostra diseguaglianza diventa quindi:
[math] 4x^2 - y + 1 > 0 [/math]
Cioè:
[math] y > 4x^2 + 1 [/math]
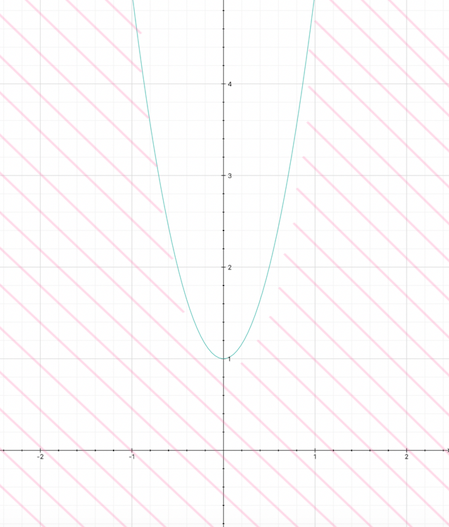
Riconosciamo in tale espressione l'equazione di una parabola con asse coincidente con l'asse verticale (
[math] y = 4x^2 + 1 [/math]
).In particolare, il segno
[math]>[/math]
(minore) ci indica che la diseguaglianza rappresenta tutti i punti del piano che si trovano al di sotto di tale parabola.
Potrebbe interessarti anche
- Numeri complessi in forma algebrica (videolezione)
- Appunti sui numeri complessi
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
