Procediamo considerando un generico numero complesso
[math]z[/math]
della forma [math] a + ib [/math]
; ricordando che il coniugato di un numero complesso equivale al numero complesso che ha stesa parte reale e parte immaginaria opposta, la nostra diseguaglianza diventa:
[math] | a + ib + (a - ib)| + | a + ib - (a - ib) | >= 2 [/math]
Svolgiamo i calcoli:
[math] | a + ib + a - ib| + | a + ib - a + ib | >= 2 [/math]
[math] | 2a | + | 2bi | >= 2 [/math]
Possiamo portare fuori dal modulo il numero 2 e semplificare:
[math] 2 | a | + 2 | bi | >= 2 [/math]
[math] | a | + | bi | >= 1 [/math]
Ricordiamo che
[math]a[/math]
e [math]b[/math]
esprimono rispettivamente la parte reale e la parte immaginaria del numero complesso [math]z[/math]
, quindi:
[math] | Re(z) | + | Im(z) | >= 1 [/math]
Ricordiamo che nel piano complesso la parte reale del numero rappresenta l'asse orizzontale, mentre la parte immaginaria l'asse verticale; ovvero :
[math] Re(z) = x , Im(z) = y [/math]
La diseguaglianza, quindi, rappresenta il quadrato descritto nel piano
[math](x;y)[/math]
dalla seguente relazione:
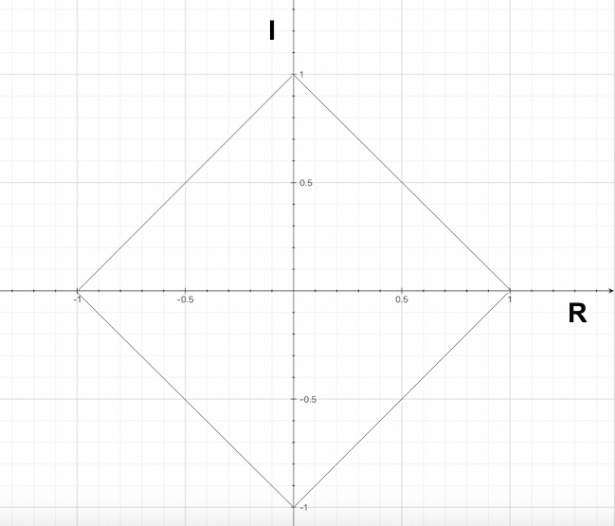
[math] | x | + | y | >= 1 [/math]
Si tratta, quindi, del quadrato che ha per vertici i seguenti punti:
[math] (0;1) , (0; -1) , (1;0) , ( -1 ;0 ) [/math]
Potrebbe interessarti anche
- Numeri complessi in forma algebrica (videolezione)
- Appunti sui numeri complessi
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
