Contrasto: somma di forze risultanti

Nel seguente appunto vedremo un esercizio relativo alle somme vettoriali, ma suddiviso in tre parti in base all'angolo che le due forze agenti formano tra di loro.
Si ricorda infatti che in generale il modulo della somma di due vettori non è uguale alla somma dei moduli! Tutto sta nell'angolo che i due vettori formano.
Si pensi ad esempio a due vettori

dello stesso modulo, della stessa direzione, ma di verso opposto.
Allora la loro somma fa 0 perché i loro effetti si "elidono", e il vettore nullo ha modulo 0, ma chiaramente la somma dei due moduli è sicuramente diversa da 0 (nell'ipotesi in cui entrambi i vettori siano di modulo non nullo, chiaramente).
Nell'esercizio seguente analizzeremo 3 (degli infiniti) casi possibili che si possono verificare quando sommiamo due vettori. Vediamo il testo dell'esercizio.

Testo dell'esercizio

Durante un contrasto in una partita di calcetto due avversari calciano il pallone contemporaneamente. Sapendo che ciascuno dei due calciatori esercita sul pallone una forza di 20N, calcola la forza risultante nei casi in cui l' angolo formato dalle due forze sia di 90°, 120° e 180°.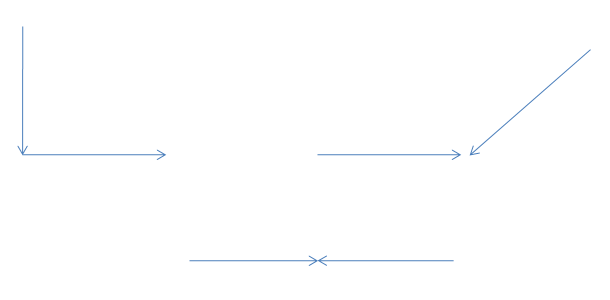

Svolgimento dell'esercizio

Nel primo caso il modulo della forza risultante coincide con la lunghezza dell'ipotenusa del triangolo rettangolo avente per cateti le due forze, perché per ipotesi l'angolo è di .
Si ha:
Nel secondo caso le due forze vanno a creare un triangolo isoscele con angoli alla base di da cui:
.
Troviamo il modulo:
Nel terzo caso, i due vettori, come detto nell'introduzione, si annullano a vicenda. Dunque