Concetti Chiave
- Una massa inizia a slittare su un blocco di ghiaccio semisferico privo di attrito dopo una piccola spinta.
- Il distacco della massa avviene a un'altezza pari a 2R/3 quando la forza normale si annulla.
- Il coseno dell'angolo tra il raggio e la direzione della forza peso si esprime come h/R.
- La velocità al punto di distacco si determina tramite l'equazione v² = g * h, derivata dalle forze centripete.
- Il bilancio energetico rivela che l'altezza di distacco è 2/3 del raggio iniziale, dimostrando il punto di separazione.
{etRating 4}
Una massa è appoggiata su un blocco di ghiaccio semisferico. Si dà una piccola spinta e questa inizia a
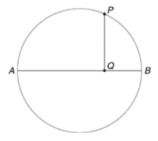
slittare sul ghiaccio. Si dimostri che, se si suppone il ghiaccio privo di attrito, tale massa si stacca ad un'altezza pari a 2R/3 (nell'istante del distacco la forza normale si deve annullare).Prima di tutto occorre disegnare la semicirconferenza di centro
Prendiamo un punto
Considerazioni energetiche: all'inizio il corpo possiede energia potenziale pari a
Nel moto circolare abbiamo che
Quindi sapendo
Ricordiamo il bilancio energetico
semplifichiamo e sommiamo per ottenre
FINE
Domande da interrogazione
- Qual è la condizione per cui la massa si stacca dal blocco di ghiaccio?
- Come si calcola la velocità della massa nel punto di stacco?
- Qual è il bilancio energetico utilizzato per determinare l'altezza di distacco?
La massa si stacca quando la forza normale si annulla, il che avviene ad un'altezza pari a 2R/3.
La velocità si calcola usando la relazione [math]v^2 = g \cdot h[/math], derivata dall'equilibrio tra forza centripeta e componente radiale della forza peso.
Il bilancio energetico è [math]m \cdot g \cdot R = m \cdot g \cdot h + 1/2 \cdot m \cdot v^2[/math], che porta a determinare [math]h = 2/3R[/math] quando si sostituisce [math]v^2 = g \cdot h[/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
