Concetti Chiave
- Calcolare le componenti cartesiane di un vettore significa scomporlo in due vettori ortogonali, utile per analizzare forze in specifiche direzioni.
- La scomposizione dei vettori aiuta a comprendere meglio concetti come la velocità verticale, che esclude lo spostamento orizzontale.
- Nell'esercizio viene richiesto di trovare le componenti cartesiane di un vettore con modulo di 4 passi e un angolo di 120° rispetto all'asse x positivo.
- Si utilizza la trigonometria per risolvere il problema, visualizzando la situazione come due triangoli rettangoli.
- Le componenti calcolate sono: ax = -2 passi e ay = 2√3 passi.
Calcolare le componenti cartesiane di un vettore significa, in fisica, scomporlo come somma di due vettori ortogonali (generalmente) tra di loro.
Tale approccio risulta utile perché, ad esempio, le forze sono grandezze vettoriali e a volte serve sapere solamente quali sono le forze che agiscono in una determinata direzione piuttosto che in un'altra perché non influenzano le altre direzioni.
O in alcuni casi la scomposizione di vettori risulta utile per poter comprendere meglio determinati concetti: la velocità verticale di un aereo, ad esempio, è quella componente di velocità che "ignora" lo spostamento orizzontale e dice quanto, invece, l'aereo sale (o scende) in una certa unità di tempo.
Nel seguente esercizio vedremo come calcolare le componenti cartesiane di un vettore, vediamo il testo.
Testo dell'esercizio
Calcola le componenti cartesiane
Soluzione dell'esercizio
Risulta utile visualizzare graficamente la situazione: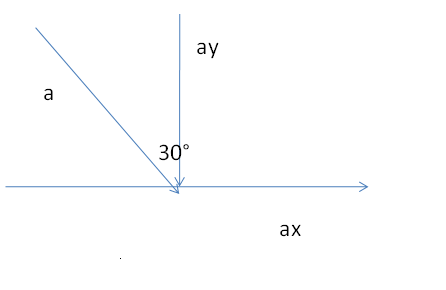 
Dall' immagine notiamo la formazione di due triangoli rettangoli sempre risolubili mediante la trigonometria:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
