
Ecco la pagina della soluzione della seconda prova di Matematica per il liceo scientifico.
Tutte le soluzioni della prova di Matematica:
In questa pagina avrete modo quindi di potere analizzare le soluzioni della prova di Matematica confrontandola con quella svolta da voi nel corso della seconda prova di Maturità del 22 giugno. Dovete tenervi quindi pronti a confrontarla con quella svolta con tanto impegno dai nostri tutor.
Mettete grande impegno nello svolgimento dei due problemi e dei vari quesiti di matematica per il liceo scientifico. La concentrazione in questo fatidico giorno dovrà essere molto alta e avrete anche la possibilità di vedere in questa pagina se avete svolto al meglio il vostro compito!
Siete pronti per questa prova? Allora cercate di svolgere al meglio la prova di matematica!
Ecco qui di seguito le prove di Matematica!
Soluzione problema 1 matematica
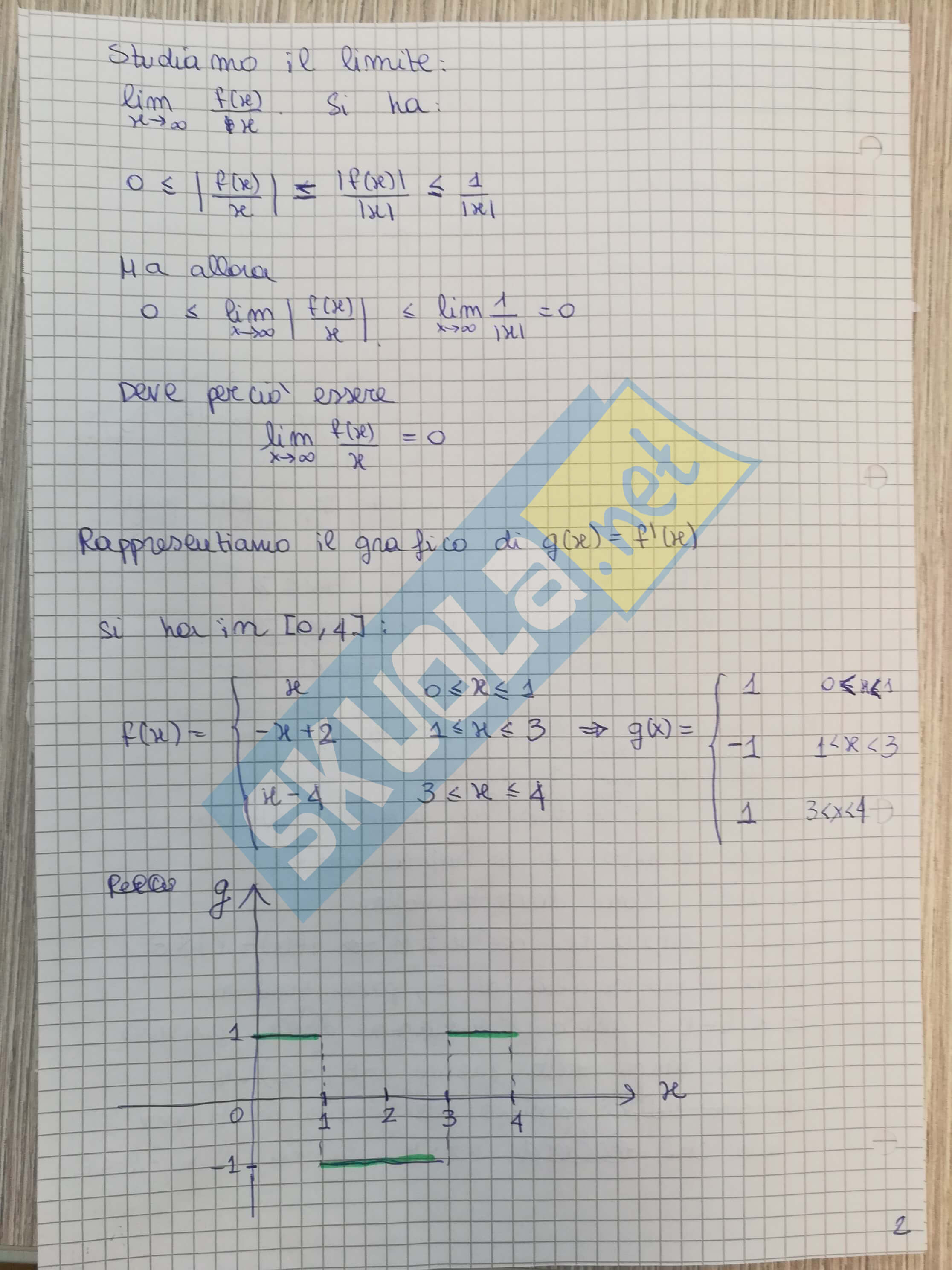
Qui troverai la soluzione del primo problema della seconda prova di matematica per il liceo scientifico con grafici, formule e studio della funzione.
Se non riesci a vedere il documento, scarica l'allegato!
Soluzione problema 2 matematica
Ecco la soluzione al problema numero 2 del testo dell'esame di stato per i licei scientifici risolto dai nostri insegnanti:





Soluzione quesiti matematica
Qui troverai nel dettaglio le soluzioni di tutti i 10 quesiti della prova d'esame di matematica risolti dai nostri insegnanti esperti.
Quesito 1

Per ipotesi
.
Vogliamo dimostrare che
.
Svolgiamo quest'ultimo integrale per parti:
Quindi avremo che:
Adesso vogliamo esprimere
in termini di e ed E.
Usando la formula di integrazione per parti, abbiamo che:
Quindi avremo che:
Quesito 2

Il cilindro e la cupola sono ottenuti dalla rotazione completa attorno all'asse y delle funzioni:
Dalla formula del volume del solido di rotazione si ha:
Si vuole mostrare che
. Dunque:
Infatti:
Quesito 3

Procedendo per sostituzione nel limite:
Quindi il numeratore deve risultare infinitesimo per
Otteniamo:
Applicando il teorema di de l'Hospital si ottiene:
Quesito 4


Il valore medio dei numeri generati si trova tramite formula per calcolare il valore atteso di un evento data la distribuzione di probabilità
:
La probabilità che il primo numero estratto sia
, invece, è una probabilità del tipo
, che è nulla nel caso di variabili casuali continue:
.
Infine, per calcolare la probabilità che il secondo numero estratto sia minore di 1, definiamo
.
Noi però vogliamo che il secondo numero estratto sia minore di (e non minore o uguale!); ma poiché
, si avrà che
e quindi
.
Quesito 5

Abbiamo i punti
,
,
.
Calcoliamo l'equazione della retta per A e B in forma parametrica con la formula
x=x_A + (x_B-x_A) \cdot t \\
y=y_A + (y_B-y_A) \cdot t \\
z=z_A + (z_B-z_A) \cdot t
\end{cases}[/math]
x = -2+5t \\
y = 3-3t \\
z = 1-2t
\end{cases}}[/math]
La direzione della retta per AB è dunque individuata dal vettore
.
Calcoliamo ora l'equazione del piano
perpendicolare alla retta trovata.
Sappiamo in generale che, se
è l'equazione di un piano, il vettore dei coefficienti (a,b,c) individua la direzione perpendicolare a tutti i vettori appartenenti al piano stesso. Quindi nel nostro caso il piano avrà equazione
.
Per trovare la costante
imponiamo il passaggio del piano per il punto
: sostituiamo le sue coordinate ed otteniamo:
Quindi l'equazione del piano cercata è
.
Quesito 6

Applicando il teorema di de L'Hospital si ottiene:
Applicando di nuovo il teorema:
avendo posto
per garantire l'esistenza. Notiamo la presenza del limite notevole
se
. Si ottiene:
Dunque la risposta è
Quesito 7

I centri appartengono alla retta passante in P ortogonale al piano
. Considerando che il vettore direttore del piano
ha componenti
, si può scrivere l'equazione della retta
:
\begin{cases}
x=1+t\\
y=2t\\
z=2-t
\end{cases}[/math]
Ora per determinare
e
occorre trovare i due punti appartenenti ad
che distano
dal punto P:
Dunque si hanno le soluzioni:
Quesito 8


Per definizione, la somma di tutte le probabilità di ciascuna faccia dev'essere 1. La probabilità che esca la faccia 3 dev'essere doppia rispetto alle altre. Chiamata
la generica probabilità che esca la faccia numero n, si ha
per
,
. Dunque la somma diventa:
da cui
Calcolare la probabilità che in 5 lanci esca la faccia numero 3 ALMENO due volte. È più agevole calcolare la probabilità dell'evento complementare, cioè quella dell'evento E_1: ''In 5 lanci del dado la faccia numero 3 esce al massimo 1 volta''. Si ha:
Tenendo presente che
dove p è la probabilità che l'evento avvenga, e q=1-p è la probabilità dell'evento complementare, otteniamo:
con
e
Infine:
Quesito 9

Per dimostrare che l'equazione
ammette un'unica soluzione reale studiamo la funzione
Essa ha come dominio tutto l'insieme
, ed è continua in tutto il suo dominio.
Studiamo il segno della sua derivata prima:
(perché è una somma con tutti addendi positivi), quindi
è strettamente crescente in tutto
.
Inoltre si ha che:
quindi la funzione, continua e strettamente crescente, assume sia valori positivi che negativi e dunque deve avere necessariamente uno zero (che è unico perché è strettamente monotona).
Quesito 10




Il teorema di Rolle afferma che, se
è continua in
, derivabile in
e tale che
, allora esiste almeno un punto
tale che
.
Vediamo se nell'intervallo
le ipotesi del teorema sono verificate per la nostra funzione
:
1)
è continua in
, in quanto composizione di funzioni continue (il polinomio
e la funzione modulo)
2)
, infatti:
3)
è non è però derivabile in
: infatti, sappiamo che la funzione
non è derivabile se il suo argomento si annulla (perché i due limiti sinistro e destro del rapporto incrementale, anche se esistono, sono diversi). Nel nostro caso, l'argomento è
, che si annulla se e solo se:
Quindi gli unici punti di non derivabilità di
(che saranno punti angolosi) sono
(negli altri punti
è derivabile perché la sua derivata
è continua per
).
Esiste comunque un punto in cui
si annulla, e lo si vede dalla forma di
:
Questo esempio comunque non contraddice il Teorema di Rolle, perché quest'ultimo ci garantisce delle condizioni \emph{sufficienti}, ma non necessarie! Se valgono le tre ipotesi, allora esiste almeno un punto in cui la derivata si annulla; ma se le tre ipotesi non valgono, può comunque esistere un punto in cui la derivata si annulla (va visto caso per caso).
Per ogni informazione, dubbio o problema, ecco i nostri recapiti:
via mail: redazione@skuola.net
tramite WhatsApp al numero 3938025594
via Twitter @skuolanet
via Facebook
Non aspettate quindi altro tempo…seguite su Skuola.net la Maturità 2017 sulla seconda prova di maturità di Matematica, come avete fatto il 21 giugno in occasione della prima prova di Maturità del 2017!







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo