In quest'appunto troverai delle informazioni generali sulla trigonometria e su come è possibile risolvere le equazioni e le disequazioni trigonometriche.
Indice
Cos'è la trigonometria e cosa studia
La matematica è composta da diverse branche: una di queste è la trigonometria. La trigonometria è la disciplina che studia le proprietà dei triangoli basate su quelle degli angoli. In particolare, attraverso le funzioni trigonometriche è possibile correlare le lunghezze caratteristiche dei triangoli (come i lati, le altezze etc.) ad altre misure.In generale, le funzioni trigonometriche sono delle funzioni periodiche: ciò significa che, con una certa cadenza, la funzione assume gli stessi valori.
Tra le funzioni trigonometriche più importante ricordiamo:
- la funzione seno [math]y=sen(x)[/math],in cui la[math]y[/math]può assumere tutti i valori inclusi tra gli estremi[math]-1[/math]e[math]1[/math]ed esiste nell'insieme dei numeri reali. La periodicità della funzione seno è[math]2\pi[/math]
- la funzione coseno [math]y=cos(x)[/math], presenta dominio e codominio uguale alla precedente funzione. La periodicità della funzione coseno è[math]2\pi[/math]
- la funzione tangente [math]y=tan(x)=\frac{sen(x)}{cos(x)}[/math], in cui la[math]y[/math]può assumere qualsiasi valore, mentre il dominio corrisponde ai numeri reali meno i valori di[math]x[/math]che annullano il coseno, cioè[math]\frac{\pi}{2}+n \pi [/math]. La periodicità della funzione seno è[math]\pi[/math]
- la funzione cotangente [math]y=cotg(x)[/math], che ha lo stesso codominio della tangente e come dominio l'insieme dei numeri reali meno i valori di[math]x[/math]che annullano il seno, ossia[math]n \pi[/math]. La periodicità della funzione cotangente è[math]\pi[/math]
- la funzione secante [math]y=sec(x)[/math], in cui la
- la funzione cosecante [math]y=cosec(x)[/math], la quale ha il codominio della funzione secante e il dominio della funzione cotangente. La periodicità della funzione cosecante è
[math]y[/math]
può assumere tutti i valori esterni all'intervallo [math][-1,1][/math]
inclusi gli estremi mentre il dominio è uguale a quello della tangente. La periodicità della funzione secante è [math]2\pi[/math]
[math]2\pi[/math]
Cosa sono le equazioni e le disequazioni trigonometriche
In matematica si definiscono equazioni le uguaglianze in cui compare, in uno dei due membri, un'incognita. Essa può trovarsi come funzione a se stante o posizionata nell'argomento di un'altra funzione. Quando in un'equazione compare una funzione trigonometrica con un'incognita nell'argomento, l'equazione prende il nome di equazione trigonometrica. Il discorso può essere esteso anche alle disequazioni.Risolvere le equazioni e le disequazioni trigonometriche elementari è facile se si conoscono le periodicità delle funzioni trigonometriche. Ad esempio, per conoscere il risultato della disequazione
[math]cos(x)>\frac{1}{2}[/math]
, bisogna prima di tutto risolvere l'equazione associata, ossia [math]cos(x)=\frac{1}{2}[/math]
.In questo caso,
[math]x=60°+2\pi[/math]
. Tuttavia, stiamo cercando i valori per cui [math]cos(x)>\frac{1}{2}[/math]
. Dalla circonferenza goniometrica possiamo vedere che il risultato di tale disequazione è [math] \frac{\pi}{3}>x>-\frac{\pi}{3}[/math]
.Il discorso si complica quando le disequazioni e le equazionitrigonometriche coinvolgono più di una funzione, per cui è essenziale sfruttare altre tecniche come quella della sostituzione. Nel prossimo paragrafo verrà approfondito il caso
[math]sin(2x)>tg(x)[/math]
Esempio: disequazione svolta e commentata con funzione sen2x
Prima di commentare il procedimento proposto nella figura, è necessario fare un piccolo appunto sulla funzione[math]sen(2x)[/math]
. E' bene sottolineare, infatti, che [math]sen(2x)\neq 2\cdot sen(x)[/math]
!Le funzioni
[math]cos(2x)[/math]
e [math]sen(2x)[/math]
hanno un proprio sviluppo, conseguenza della formula di duplicazione del seno e del coseno. In particolare:- [math]sen(2x)=2sin(x)cos(x)[/math]
- [math]cos(2x)=cos^2(x)-sen^2(x)[/math]
Come mostrato dalla figura in basso, il primo step da svolgere per risolvere la disequazione è sviluppare attraverso la formula della duplicazione la funzione
[math]2sen(x)cos(x)[/math]
e scrivere la funzione tangente come il rapporto tra la funzione seno e la funzione coseno. Così facendo, è possibile eseguire un raccoglimento totale raccogliendo [math]cos(x)[/math]
.A questo punto, al primo membro compare il prodotto tra funzioni
[math]\frac{sen(x)}{cos(x)}\cdot(2cos^2(x)-1)[/math]
. La disequazione è soddisfatta se questo prodotto è positivo, cioè se i fattori sono entrambi positivi o entrambi negativi.
Studiando il segno delle singole funzioni è possibile comprendere per quali valori di [math]x[/math]
le due funzioni sono concordi. La soluzione finale è quindi [math]\frac{\pi}{3}>x>\frac{\pi}{2}, \frac{\pi}{2}>x>\frac{2\pi}{3}, \pi>x>\frac{4\pi}{3}, \frac{3\pi}{2}>x>\frac{5\pi}{3}[/math]
.
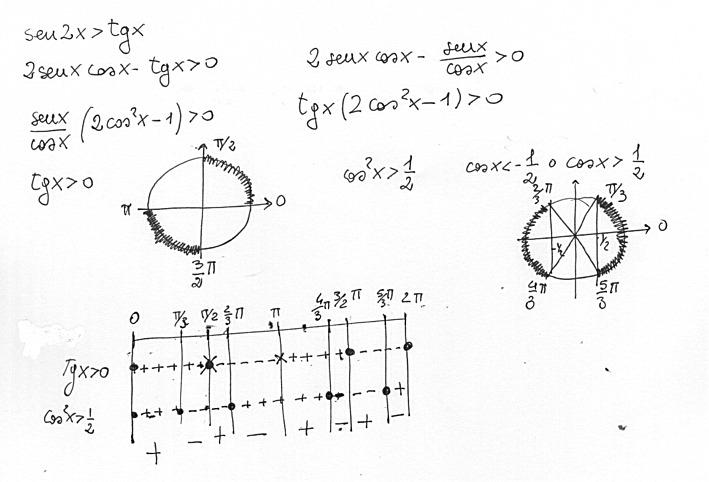
Per ulteriori approfondimenti sulle disequazioni trigonometriche vedi anche qui
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
