Individuare il vertice C di un triangolo isoscele di base AB con
[math]A(-1;1)[/math]
e [math]B(2;0)[/math]
, sapendo che l'altezza relativa ad AB misura [math](\sqrt10)/2[/math]
Iniziamo a calcolare l'equazione della retta su cui giace la base.
Il coefficiente angolare della retta passante per due punti noti (nel nostro caso
[math]A[/math]
e [math]B[/math]
) vale
[math]m=(y-y_0)/(x-x_0)[/math]
ovvero, nel caso nostro
[math]m=-1/3[/math]
Il fascio generico è
[math]y-y_0=m(x-x_0)[/math]
quindi sostituendo i valori noti di
[math]m[/math]
e quelli di [math]x_0,y_0[/math]
(un punto vale l'altro) otteniamo che la retta
[math]AB[/math]
ha equazione
[math]y=-x/3+2/3[/math]
. La retta
[math]CH[/math]
ha coefficiente angolare pari a [math]3[/math]
essendo perpendicolare alla retta [math]AB[/math]
e passa per il punto medio del segmento [math]ar(AB)[/math]
Le coordinate del punto medio
[math]H[/math]
sono facilmente ricavabili, ricordiamo che le coordinate sono
[math]H((x_1+x_2)/2,(y_1+y_2)/2)[/math]
da cui abbiamo che H è pari a
[math]H=(1/2,1/2)[/math]
per cui la retta
[math]CH[/math]
è:
[math]y-1/2=3(x-1/2)[/math]
ovvero
[math]y=3x-1[/math]
. (abbiamo applicato le note formule sui fasci di rette conoscendo un punto e il coefficiente angolare, come sopra).
Quindi
[math]C[/math]
ha coordinate generiche [math](a,3a-1)[/math]
. Ma sappiamo che la distanza di
[math]C[/math]
da [math]H[/math]
è pari a
[math](\sqrt10)/2[/math]
, cioè, applicando la formula della distanza tra due punti
[math]\sqrt{(a-1/2)^2+(3a-3/2)^2}=(\sqrt10)/2[/math]
ovvero
[math](a-1/2)^2+(3a-3/2)^2=10/4[/math]
svolgendo
[math]10a^2-10a=0[/math]
e restituisce
[math]a=0,a=1[/math]
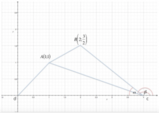
. Ora
[math]a=0->C=(0,-1)[/math]
mentre
[math]a=1->C=(1,2)[/math]
FINE
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
