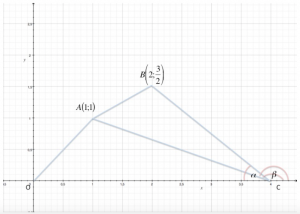
Il quadrilatero
[math]OABC[/math]
ha vertici in [math]O(0;0)[/math]
, [math]A(1;1)[/math]
, [math]B (2 ; 3/2)[/math]
, e il vertice [math]C[/math]
sul semiasse positivo delle [math]x[/math]
. Sapendo che , detta [math] alpha[/math]
l'ampiezza dell'angolo [math]hat{OCB}[/math]
, risulta [math] tg(alpha) = 3/4[/math]
, determinare le coordinate di [math]C[/math]
e le tangenti degli angoli [math]hat{OCA}[/math]
e [math]hat{ACB}[/math]
.
Svolgimento
Sapendo che[math] tg(alpha) = 3/4[/math]
possiamo affermare che il coefficiente angolare della retta [math]BC[/math]
è
[math] m = - tg(alpha) = - 3/4 [/math]
Possiamo trovare l'equazione della retta
[math]BC[/math]
:
[math] BC : y - y_0 = m (x - x_0 ) \to y - 3/2 = - 3/4 (x - 2 )[/math]
[math] y - 3/2 = - 3/4 x + 3/2 \to 4y - 6 = - 3x + 6 [/math]
[math] BC : 3x + 4y - 12 = 0 [/math]
Possiamo trovare le coordinate del punto
[math]C[/math]
sapendo che esso è il punto di intersezione della retta [math]BC[/math]
con l'asse [math]x[/math]
:
[math] BC â© y = 0 [/math]
[math][/math]
left{ \begin{array}{rl}
3x + 4y - 12 = 0 &\
y = 0 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
3x + 4y - 12 = 0 &\
y = 0 &
end{array}\right.
[math][/math]
Sostituendo il valore di
[math]y[/math]
nella prima equazione si ottiene:
[math][/math]
left{ \begin{array}{rl}
x = 4 &\
y = 0 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
x = 4 &\
y = 0 &
end{array}\right.
[math][/math]
Abbiamo quindi il punto
[math]C[/math]
di coordinate [math](4;0)[/math]
.Ora, l'angolo
[math]hat{OCA}[/math]
è il supplementare dell'angolo [math]\beta[/math]
che la retta [math]AC[/math]
forma con la direzione positiva dell'asse [math]x[/math]
, e poiché la retta [math]AC[/math]
ha coefficiente angolare [math]- 1/3[/math]
, si ha che:
[math] tg(hat{OCA}) = - tg(\beta) = - (- 1/3) = 1/3 [/math]
Possiamo trovare la tangente dell'angolo
[math]hat{ACB}[/math]
utilizzando la formula
[math] tg(x) = frac(m - m')(1 + m m') [/math]
sapendo che l'angolo in questione è formato dalle rette
[math]AC[/math]
e [math]CB[/math]
, di coefficiente angolare rispettivamente uguale a [math]- 1/3[/math]
e [math]- 3/4[/math]
:
[math] tg(hat{ACB}) = frac( -1/3 - (- 3/4))(1 - 1/3 \cdot (- 3/4)) = frac(- 1/3 + 3/4)(1 + 1/4) = [/math]
[math] frac(frac(-4+9)(12))(frac(4+1)(4)) = frac(5)(12) \cdot 4/5 = 1/3 [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
