Verificare che il triangolo di vertici
[math]A(3;2); B(6;1); C(5;4)[/math]
è isoscele. Svolgimento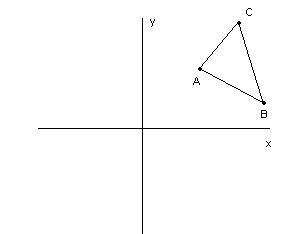
Dobbiamo dimostrare che due segmenti sono uguali tra loro.
Calcoliamo le misure dei tre segmenti
[math]ar(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt((6-3)^2+(1-2)^2)=\sqrt(9+1)=\sqrt(10)[/math]
[math]ar(BC)=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}=\sqrt((5-6)^2+(4-1)^2)=\sqrt(1+9)=\sqrt(10)[/math]
[math]ar(AC)=\sqrt{(x_3-x_1)^2+(y_3-y_1)^2}=\sqrt((5-3)^2+(4-2)^2)=\sqrt(4+4)=\sqrt(8)=2\sqrt2[/math]
Quindi, essendo
[math]ar(AB)=ar(AC)=\sqrt{10}[/math]
, il triangolo [math]hat{ABC}[/math]
è isoscele.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
