[math]\hat{ABC}[/math]
di base
[math]\bar{AB}[/math]
si prolunghi il lato
[math]\bar{AC}[/math]
di un segmento
[math]\bar{CE}[/math]
dalla parte di
[math]C[/math]
e si prolunghi
[math]\bar{BC}[/math]
di un segmento
[math]\bar{CD}[/math]
dalla parte di
[math]C[/math]
,in modo che
[math]\bar{CE}~=\bar{CD}[/math]
.
Sia
[math]F[/math]
il punto d'intersezione di
[math]\bar{AD}[/math]
con
[math]\bar{EB}[/math]
. Dimostrare che
[math]hat{ABF}[/math]
.
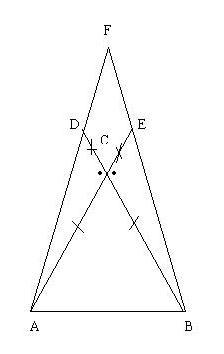
Ipotesi
[math]\bar{AC}~=\bar{CB}[/math]
[math]\bar{CE}~=\bar{CD}[/math]
Tesi
[math]\hat{ABF}[/math]
isoscele
Dimostrazione
[math]\hat{ACD}~=\hat{BCE}[/math]
per il primo criterio, infatti
[math]\bar{AC}~=\bar{CB}[/math]
per costruzione
[math]\bar{CE}~=\bar{CD}[/math]
per costruzione
[math]D\hat{CA}~=E\hat{CB}[/math]
perchè opposti al vertice
Di conseguenza
[math]D\hat{AC}~=E\hat{BE}[/math]
. Pertanto
[math]F\hat{AB}~=F\hat{BA}[/math]
, perchè somma di angoli congruenti, infatti
[math]F\hat{AB}=F\hat{AC}+C\hat{AB}[/math]
e
[math]F\hat{BA}=F\hat{BC}+C\hat{BA}[/math]
, dove
[math]F\hat{AC}~=F\hat{BC}[/math]
e
[math]C\hat{AB}~=C\hat{BA}[/math]
.
Quindi la tesi.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
