In questo appunto viene spiegato e risolto il problema che prevede il calcolo del perimetro di un trapezio rettangolo e della sua diagonale minore sapendo che la diagonale minore forma un angolo retto con il lato obliquo.
Richiamiamo brevemente prima dei concetti che ci saranno utili poi nello svolgimento del problema.
Indice
Il trapezio: definizione, caratteristiche e area
Il trapezio è una figura piana costituita da due lati paralleli, chiamati base minore e base maggiore, e da due lati obliqui.
Nel problema si considera un trapezio rettangolo ovvero un trapezio che oltre ad avere due lati paralleli (le basi), possiede uno dei due lati obliqui disposto perpendicolarmente rispetto alle due basi.
Nel trapezio è possibile individuare due diagonali (segmenti che congiungono i vertici opposti quindi non adiacenti), nel caso di trapezio generico e di trapezio rettangolo queste due diagonali hanno lunghezze differenti perciò prendono il nome di diagonale maggiore e diagonale minore, nel caso di trapezi più particolare come quello isoscele e come il rettangolo, tali due diagonali hanno la stessa lunghezza perciò sono equivalenti.
Il perimetro del trapezio si trova sommando tutti i lati del trapezio quindi è necessario sommare le due basi e i due lati obliqui.
Per ulteriori approfondimenti sul trapezio e sulle sue caratteristiche vedi anche qua
Teorema di Pitagora: spiegazione e formula
Nel problema vedremo che sarà necessario utilizzare il teorema di Pitagora, perciò ora richiamiamo brevemente tale teorema.
Il teorema di Pitagora è valido solo nel caso di triangoli rettangoli (triangoli che possiedono un angolo retto ovvero due lati sono disposti a 90° tra loro), nel caso di triangoli rettangoli i lati assumono dei nomi specifici: si definiscono cateti i due lati che formano un angolo retto, mentre di chiama ipotenusa il lato che è opposto all’angolo retto.
Dato un triangolo rettangolo, il teorema di Pitagora afferma che:
La formula esprime che il quadrato costruito sull’ipotenusa ha un valore equivalente alla somma dei quadrati costruiti sui cateti.
Per ulteriori approfondimenti sul teorema di Pitagora vedi anche qua
Svolgimento del problema:
Il testo del problema è riportato in seguito:
In un trapezio rettangolo ABCD la lunghezza della differenza delle basi è 36cm; essa corrisponde ai
della lunghezza della base maggiore.
Sapendo che la diagonale minore è perpendicolare al lato obliquo e che la lunghezza della base maggiore corrisponde ai
della lunghezza del lato obliquo, calcola il perimetro del trapezio e la lunghezza della diagonale.
Proviamo come prima cosa a riscrivere con relazioni matematiche i dati che vengono riportati nel problema.
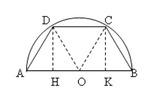
Consideriamo un trapezio rettangolo: figura piana caratterizzata da due lati paralleli (le basi), da un lato perpendicolare alle due basi e da un generico lato obliquo.
Chiamiamo
la base maggiore e
la base minore.
Il problema afferma che la lunghezza della differenza tra le basi è 36cm perciò riscritto sottoforma di uguaglianza matematica corrisponde a:
Tale differenza (36cm) corrisponde ai
della base maggiore (
) perciò:
Possiamo quindi immediatamente calcolare il valore della base maggiore
esplicitandolo nell’equazione precedente e svolgendo i prodotti.
Il problema afferma inoltre che la diagonale minore (
) è perpendicolare al lato obliquo (
), i due lati formano un angolo retto perciò l’angolo
ha un’ampiezza di 90°.
Il problema ci dice inoltre che la lunghezza della base maggiore (
) è
della lunghezza del lato obliquo (
), perciò:
Abbiamo già trovato che la base maggiore è lunga 100cm, perciò possiamo calcolare il valore del lato obliquo: si esplicita il lato obliquo
nella relazione, si sostituisce il valore di
che abbiamo trovato in precedenza e si svolgono i calcoli come segue:
Il problema richiede il valore del perimetro: abbiamo già trovato i valori del lato obliquo e della base maggiore perciò ora calcoliamo prima il valore della base minore e poi il valore del lato ortogonale alle due basi.
Per calcolare il valore della base minore possiamo considerare che la base maggiore (
) è lunga 100cm e che la differenza delle basi è 36 cm quindi:
Si esplicita l’incognita
, si sostituisce il valore di
e si eseguono i calcoli come segue:
Proseguiamo ora con il calcolo dell’altezza: se si traccia l’altezza (
) passante per il vertice C adiacente al lato obliquo si può notare che il triangolo CHB è rettangolo con l’angolo retto posizionato nel vertice C, in questo caso la differenza delle basi coincide proprio con il segmento
.
Dato che si sta considerando un triangolo rettangolo è possibile utilizzare il teorema di Pitagora perciò si avrà che:
Da questa relazione esplicitiamo
che è la grandezza che dobbiamo calcolare, sostituiamo i valori di
e
ed eseguiamo i calcoli:
Quindi:
In un trapezio rettangolo l’altezza è equivalente al lato perpendicolare alle basi perciò
Ora che abbiamo trovato la lunghezza di tutti i lati possiamo sommarli e calcolare il perimetro:
Per calcolare la lunghezza della diagonale minore sfruttiamo il fatto che tale diagonale forma una angolo retto con il lato obliquo perciò il triangolo ACB è rettangolo in C, anche in questo caso è quindi possibile applicare il teorema di Pitagora perciò:
Esplicitiamo l’incognita AC ed eseguiamo i calcoli:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
