[math]2/7 ar{AB} +2/3 ar{AD}=36cm[/math]
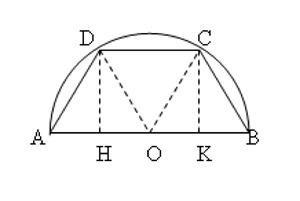
Pongo
[math]ar{AB}=x[/math]
si ha
[math]ar{AD}=1/2 x[/math]
Sostituendo nella relazione data si ha
[math]2/7 x + 2/3 \cdot 1/2 x =2,6 >/p> >p> [/math]
2/7 x +1/3 x =2,6
[math] >/p> >p> m.c.m.=21 >/p> >p> [/math]
6x+7x=54,6
[math] >/p> >p> [/math]
x=frac{54,6}{13} = 4,2cm
[math] >/p> >p> [/math]
ar{AB}=4,2cm
[math] >/p> >p> [/math]
ar{AD}=2,1cm
[math] >/p> >p> AOD è un triangolo equilatero di la o [/math]
l=2,1cm
[math] >/p> >p> [/math]
ar{DH}=l/2 sqrt(3) = frac{2,1}{2}*sqrt(3)=1,81cm
[math] >/p> >p> [/math]
AH=l/2 = frac{2,1}{2}=1,05
[math] >/p> >p> [/math]
DC=AB-2AH=2l-2*l/2=l=2,1cm
[math] >/p> >p> [/math]
2p(ABCD)=5*2,1cm=10,5cm
[math] >/p> >p> [/math]
A(ABCD)=frac{(4,2+2,1)*1,82}{2}=5,72cm^2
[math] [/p[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
