In questo appunto verrà approfondito il concetto di circonferenza, spiegando il calcolo della misura di essa a partire da alcuni elementi noti come ad esempio il raggio. Si analizzeranno anche degli esempi pratici a riguardo, spiegati passo per passo.
Indice
Che cos'è la circonferenza?
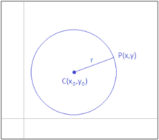
Si definisce circonferenza l'insieme di tutti i punti del piano che hanno la stessa distanza da un punto fisso[math]O[/math]
detto centro.La distanza tra il centro
[math]O[/math]
ed ogni punto della circonferenza si chiama raggio, e solitamente si indica con il simbolo r. E' evidente che una circonferenza ha infiniti raggi tutti uguali fra loro.Per individuare una circonferenza è quindi sufficiente fornire la posizione del centro
[math]O[/math]
e la misura del suo raggio. E' evidente che due circonferenze aventi lo stesso raggio sono uguali, e viceversa.
Punti interni ed esterni alla circonferenza
Tutti i punti del piano che hanno dal centro[math] O [/math]
minore distanza del raggio si dicono interni alla circonferenza. Tutti i punti che hanno dal centro [math] O [/math]
maggiore distanza del raggio si dicono esterni alla circonferenza.Naturalmente, tutti i punti che hanno distanza dal centro
[math] O [/math]
uguale al raggio sono sulla circonferenza.
Corda di una circonferenza
Congiungendo due punti qualsiasi della circonferenza si ottiene un segmento, che prende il nome di corda. Le corde di una circonferenza hanno lunghezza differente, a seconda di quanto i due punti della circonferenza che esse congiungono siano vicini o lontani.Ogni corda che passa per il centro
[math]O[/math]
della circonferenza si chiama diametro, e solitamente si indica con il simbolo D. E' evidente che una circonferenza ha infiniti diametri tutti uguali fra loro. La loro ampiezza è pari a due volte il raggio (D= 2r). Altrettanto evidente è che i diametri sono, su quella circonferenza, le corde di ampiezza massima.
Misurazione di una circonferenza
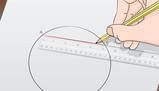
Misurare il raggio o il diametro di una circonferenza è piuttosto facile. Non altrettanto facile è determinare invece la lunghezza della circonferenza. Questo perchè l'unità di misura di cui ci serviamo è un segmento, ed è assai difficile stabilire quante volte un segmento è contenuto in una linea curva.Per risolvere il problema si possono usare varie tecniche. Una di esse consiste ad esempio nel "rettificare la circonferenza", cioè nel far aderire alla circonferenza un filo. Terminata l'operazione, si potrà tendere il filo in modo da formare una linea retta lunga quanto la circonferenza di partenza. A questo punto per determinare la misura della circonferenza sarà sufficiente misurare il filo.
Un rapporto interessante
Con questa tecnica è possibile misurare tante circonferenze di lunghezza differente. Se proviamo a dividere la misura di queste circonferenze per la misura del loro rispettivo diametro, ci accorgiamo di un fatto molto interessante. E cioè che il rapporto (o quoziente) tra la lunghezza di una circonferenza e quella del proprio diametro ha sempre lo stesso valore.A questo valore si dà il nome di "pi-greco", e viene appunto indicato con il simbolo π dell'alfabeto greco.
[math]\pi[/math]
è un numero irrazionale (cioè un numero con infinite cifre decimali e che non è possibile scrivere sotto forma di frazione). Il suo valore è pari a: [math]\pi = 3,14159265...[/math]
Normalmente esso viene approssimato al valore:
[math]π = 3,14[/math]
Stando così le cose...
[math]\frac{C}{D} = π[/math]
...possiamo scrivere che:
[math]C= D \cdot π[/math]
Oppure, ricordando che D= 2r:
[math]C= 2r \cdot π[/math]
Conclusione
La conclusione è la seguente: la lunghezza di una circonferenza è pari alla misura del suo diametro per[math]\pi[/math]
(circa 3,14), oppure alla misura del suo raggio per [math] 2\pi[/math]
( circa 6,28)Delle formule appena viste è possibile servirsi anche per calcolare il raggio o il diametro di una circonferenza qualora venga fornita la misura della circonferenza stessa:
[math]D =\frac{C}{\pi}[/math]
[math]r =\frac{C}{2\pi}[/math]
Esercizio di esempio 1
Una circonferenza misura[math]12,56 \text{cm}[/math]
. Quanto è lungo il suo raggio?
Svolgimento
L'unico dato a nostra disposizione è[math]C = 12,56 \text{cm} [/math]
. Utilizziamo la formula inversa opportuna, ossia, dato che ci viene richiesto il raggio [math]r[/math]
, usiamo la formula [math]r = \frac{C}{2 \pi} = \frac{12,56 \text{cm}}{6,28} = 2 \text{cm}[/math]
.Il raggio della circonferenza ha quindi misura
[math]2 \text{cm}[/math]
. Si precisa che tutte le misure trovate non sono esatte, in quanto [math]\pi[/math]
non vale esattamente [math]3,14[/math]
ma circa[math]3,14[/math]
.
Esercizio di esempio 2
Un cerchio ha l'area di[math]78,5 \text{cm}^2[/math]
. Qual è la misura della sua circonferenza?
Svolgimento
In questo caso c'è un passaggio ulteriore da fare. Bisogna risalire al raggio tramite la formula inversa per il calcolo dell'area del cerchio, ossia, dato che[math]A=r^2 \pi[/math]
, allora [math] r = \sqrt{\frac{A}{\pi}} [/math]
.Otteniamo dunque
[math] r = \sqrt{\frac{78,5 \text{cm}^2}{3,14}} = 5 \text{cm} [/math]
.Infine abbiamo
[math] C = 2 \pi r = 6,28 \cdot 5 \text{cm} = 31,4 \text{cm} [/math]
.Ancora una volta, non si tratta di misure esatte, bensì di misure approssimate (comunque, in maniera buona).
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
