Area del trapezio: dimostrazione della formula

In questo appunto di geometria euclidea del piano, vi propongo la dimostrazione della formula valida per calcolare l'area del quadrilatero trapezio, di qualunque tipo esso sia: scaleno, isoscele o rettangolo. La formula deriva dall’equivalenza tra le superfici del trapezio e del triangolo e si dimostra con il secondo criterio di congruenza dei triangoli. I disegni sono un valido alleato per la comprensione dei vari passaggi e un problema applicativo conclusivo per fissare le idee.

Elementi del quadrilatero trapezio

Si definisce [utrapezio un quadrilatero che ha una coppia di lati paralleli.Questi due lati paralleli vengono definiti Basi del trapezio (il maggiore dei due è denominato Base maggiore il minore è detto invece Base minore.

Gli altri due lati si dicono comunemente lati obliqui. La distanza tra le due basi (ovvero il segmento perpendicolare ad entrambe le basi) si chiama altezza del trapezio.

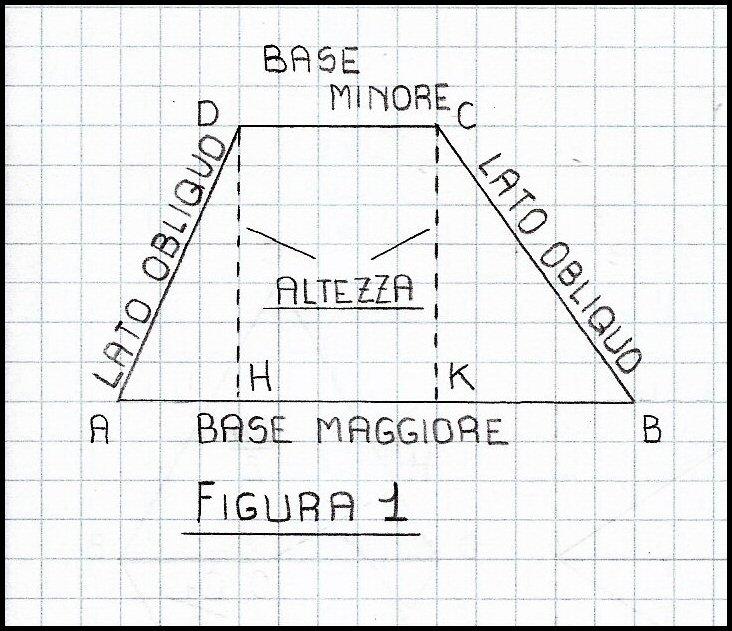
Facciamo riferimento alla Figura 1, in cui è rappresentato il trapezio ABCD, possiamo individuare i suoi elementi caratteristici:

• AB è la base maggiore indicata con B;
• CD è la base minore indicata con b;
• DH o CK sono altezze indicate con H, oppure h;
• AD e BC sono lati obliqui indicati con
  [math]L_1[/math]
  ed
  [math]L_2[/math]

Equivalenza trapezio e triangolo

Facciamo ora riferimento alla Figura 2 e procediamo come segue. Prolunghiamo la base AB di un segmento BE lungo quanto la base minore CD. Congiungiamo il punto E con il punto D, ed indichiamo con F il punto in cui il segmento ED taglia il lato obliquo BC. Congiungendo i vertici A, E, D, si ottiene il triangolo AED

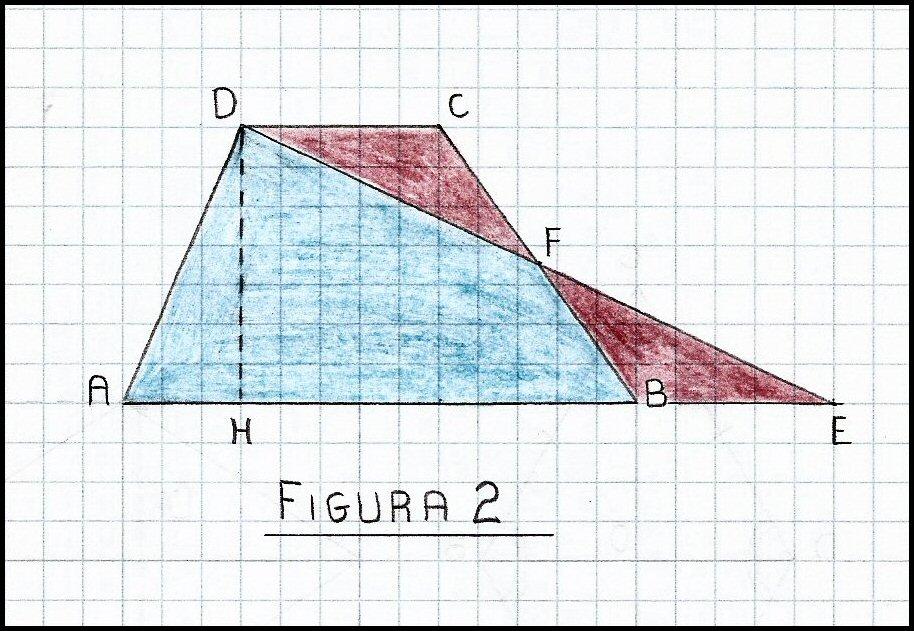
Consideriamo come base di questo triangolo il segmento AE che è pari alla somma della base maggiore AB del trapezio e, del prolungamento BE congruente alla base minore CD per costruzione, sappiamo quindi che AE=AB+CD. L'altezza relativa a questa base è il segmento DH coincidente con l'altezza del trapezio. Poiché l'area di un triangolo è data dal prodotto della sua base per la sua altezza diviso due, ponendo:

essendo poi

possiamo scrivere che:

Osserviamo ancora con attenzione la Figura 2, l’area del triangolo AED è la somma di due aree, quella del quadrilatero ABFD (in azzurro) e quella triangolo BEF (in rosso) per cui:

L’area del trapezio è somma dell’area dello stesso quadrilatero ABFD più quella del triangolo CDF:

Equivalenza tra superfici piane

Prima di effettuare la dimostrazione della formula dell’area del trapezio ripassiamo la relazione di equivalenza. L’estensione di una superficie è un concetto primitivo, al pari di altri concetti intuitivi e non definibili quali il punto, la retta e il piano. Confrontano due superfici siamo però in grado di stabilire se sono diverse oppure se sono uguali, in tal caso diciamo che le due superfici sono equivalenti, hanno cioè la stessa estensione e si dicono anche equiestese. L’equivalenza tra superfici si rappresenta con il simbolo

ed è una relazione in quanto gode delle proprietà: riflessiva, simmetrica e transitiva.
Dette

tre superfici piane, si ha infatti:

• per la proprietà riflessiva:
  [math]S\equiv S[/math]
• per la proprietà simmetrica: se
  [math]S\equiv S_1 \to S_1\equiv S[/math]
• per la proprietà transitiva: se
  [math]S\equiv S_1 \ \ e \ \ S_1\equiv S_2 \to S\equiv S_2[/math]

Ricordiamo ora i seguenti postulati di equivalenza:

• due superfici congruenti sono sempre equivalenti, e non vale il viceversa
• superfici ottenute come somme o differenze di superfici rispettivamente equivalenti sono equivalenti
• una superficie non può essere equivalente a una sua parte Postulato di De Zolt

Dimostrazione della formula dell’area

Dimostriamo allora che i due triangoli BFE e CDF sono congruenti, in tal modo per il secondo postulato soprascritto, possiamo stabilire l’equivalenza tra il triangolo AED e il trapezio ABCD. Vediamo insieme:

Consideriamo i due triangoli BFE e CDF, essi hanno:

per costruzione;

, perché angoli alterni interni congruenti formati dalle parallele AE e CD tagliate dalla trasversaleBC;

, perché angoli alterni interni congruenti formati dalle parallele AE e CD tagliate dalla trasversale DE.
I due triangoli BFE e CDF sono allora congruenti per il secondo criterio, avendo congruenti un lato e i due angoli ad esso adiacenti. Dimostrata la congruenza, per il primo postulato di cui sopra, i triangoli sono anche equivalenti.
Abbiamo allora dimostrato che il trapezio ABCD è equivalente al triangolo AED. Possiamo allora affermare che, in generale:un trapezio è equivalente ad un triangolo che ha la base uguale alla somma delle basi del trapezio ed uguale altezza.
Scriviamo in simboli matematici:

Formule inverse dell’area del trapezio

Ne derivano le seguenti formule inverse, utili per calcolare di volta in volta la somma delle basi, ciascuna base oppure l’altezza:

• [math](B+b)=\frac{2\cdot Area}{H}[/math]
• [math]H=\frac{2Area}{(B+ b)}[/math]
• [math]B=\frac{2\cdot Area}{H}-b[/math]
• [math]b=\frac{2\cdot Area}{H}-B[/math]

Applicazione numerica

Vediamo insieme un esempio pratico: si tratta di un tipo di esercizio frequentemente richiesto.
"Calcolare l'area di un trapezio sapendo che le sue basi misurano rispettivamente 24 cm e 14 cm e l'altezza è i 3/5 della differenza delle due basi".

Svolgimento:
Sono note le misure delle due basi ed è fornita la relazione tra l’altezza e la differenza delle basi. Determiniamo allora il valore di H:

Non ci resta che applicare la formula vista sopra:

inseriamo i valori numerici:

Annotazione finale

Tra tutti i possibili tipi di trapezio esistenti, ce ne sono due che godono di proprietà e caratteristiche particolari: il trapezio isoscele e il trapezio rettangolo. Il primo è un trapezio che ha i due lati obliqui uguali, mentre il secondo è un trapezio che ha uno dei due lati obliqui perpendicolare alle due basi.
In questi due trapezi la determinazione delle misure dei quattro lati (le due basi e i due lati obliqui) è molto più semplice che in un trapezio generico (e di conseguenza lo è anche il calcolo di area e perimetro), in quanto è possibile utilizzare con essi il Teorema di Pitagora.

per ulteriori approfondimenti sul trapezio isoscele vedi anche qua

per ulteriori approfondimenti sul trapezio rettangolo vedi anche qua