Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
Scarica il documento per vederlo tutto.
vuoi
o PayPal
tutte le volte che vuoi
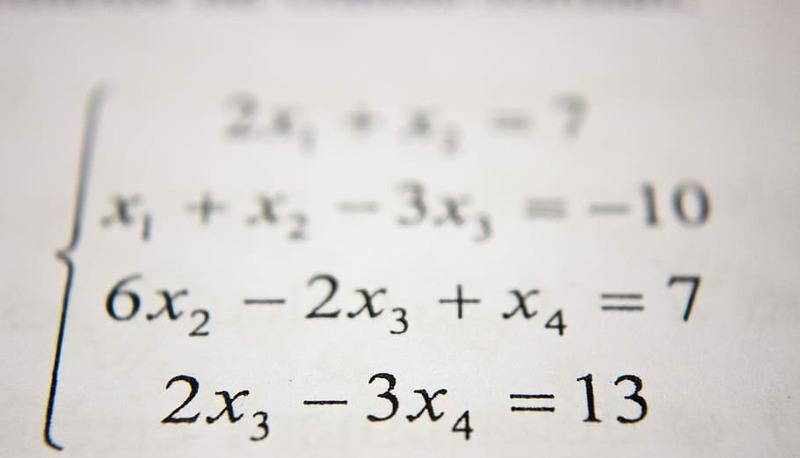
Nozioni principali di matematica - Sommario
Nel seguente appunto analizzeremo brevemente:
- Le equazioni di secondo grado;
- La geometria analitica: l'equazione di una retta, i punti, il calcolo delle distanze tra gli enti geometrici;
- Geometria euclidea: similitudine e congruenza tra i triangoli;
- Il valore assoluto;
- Logaritmi ed esponenziali;
- Coniche: ellisse, iperbole, parabola e circonferenza;
- Teoremi principali di trigonometria;
- Numeri complessi.
Equazioni e disequazioni di secondo grado
Un'equazione di secondo grado è un'espressione del tipo:
La quantità
La somma delle soluzioni di un'equazione di secondo grado è data da
Geometria analitica
Un punto (nonché un ente primitivo della geometria euclidea) nel piano cartesiano è determinato da due valori reali
La retta, in geometria analitica, è un'espressione del tipo:
dove m è detto coefficiente angolare, q è detta intercetta (oppure ordinata all'origine).
In particolare, esistono due possibili forme per scrivere l'equazione di una retta. La forma implicita di una retta è:
dove
Dati due punti
Risulta possibile anche definire la distanza tra un punto e una retta. Essa è infatti definita come la lunghezza del più piccolo segmento che congiunge tale punto con un punto della retta. Tale distanza si calcola con la formula:
dove
Geometria euclidea
Partiamo con il dare la definizione di triangolo. Un triangolo è un poligono avente tre lati e tre angoli.
Esistono infiniti triangoli, tuttavia è possibile stabilire delle relazioni tra due triangoli. In particolare, confrontando due triangoli potremo dire che:
- essi sono simili se hanno tutti e tre gli angoli rispettivamente congruenti e i tre lati tutti in proporzione con un certo rapporto. Tale rapporto è chiamato rapporto di similitudine;
- essi sono congruenti se hanno tutti e tre gli angoli rispettivamente congruenti e tutti e tre i lati congruenti.
Da queste definizioni possiamo dire che se due triangoli sono congruenti, allora sono anche simili (con rapporto di similitudine unitario); ma se due triangoli sono simili, non è detto che siano congruenti.
Per approfondimenti sui criteri di similitudine, vedi anche qua
Il valore assoluto (o modulo)
Il valore assoluto di un numero reale
In particolare nei reali positivi:
Mentre nei reali negativi:
Notiamo quindi che il valore assoluto non può mai essere negativo e restituisce il numero ottenuto "senza tenere conto del suo segno". Ad esempio
Logaritmi ed esponenziali
Dato un numero reale positivo
Si scrive come
Esistono dei logaritmi "molto usati". Essi sono il logaritmo in base 10 (molto utile in chimica) e il logaritmo naturale, ossia il logaritmo in base
Una funzione esponenziale è una qualsiasi funzione del tipo
Le coniche
In geometria analitica, risultano oggetto di studio le coniche, ossia delle curve ottenute come intersezione tra un piano e un cono. Le coniche principali sono:
- la parabola: essa ha equazione [math] y = ax^2 + bx + c[/math]ed è il luogo geometrico dei punti che hanno la stessa distanza da un punto fisso detto fuoco e una retta detta direttrice;
- l'ellisse: ha equazione [math]\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 [/math]ed è il luogo geometrico dei punti che hanno la somma delle distanze da due punti fissi detti fuochi costante.
- l'iperbole: ha equazione [math] \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 [/math]ed è il luogo geometrico dei punti che hanno la differenza tra le distanze da due punti fissi detti fuochi costante.
- la circonferenza: ha equazione [math]x^2 + y^2 + ax + by + c = 0[/math]ed è il luogo geometrico dei punti che hanno la stessa distanza da un punto fisso detto centro.
Notiamo che la circonferenza può essere vista come un caso particolare di ellisse, difatti, in questo caso, è come se i due fuochi dell'ellisse coincidessero con il centro della circonferenza!
Teoremi principali di trigonometria
La trigonometria è quel settore della matematica che studia i triangoli, non necessariamente rettangoli anche se seno e coseno sono strettamente correlati ad essi. Di seguito elenchiamo alcuni teoremi importanti e molto usati in trigonometria:
- Teorema della corda: data una circonferenza di raggio [math] r [/math]e una corda[math] AB [/math]della circonferenza in questione, vale[math] AB = 2R \sin(\alpha) [/math]dove[math] \alpha [/math]è l'angolo che insiste sulla corda[math] AB [/math].
- Teorema dei seni: in un triangolo il rapporto tra la misura di un lato e il seno dell'angolo ad esso opposto è costante e pari al diametro del cerchio circoscritto al triangolo. In formule: [math] \frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)} = 2R [/math].
- Teorema di Carnot: in un triangolo il lato opposto ad un certo angolo [math] \alpha [/math]è pari alla radice quadrata della somma dei quadrati degli altri due lati, meno il doppio prodotto tra i due lati e il coseno dell'angolo[math] \alpha [/math]. In formule:[math] c = \sqrt{a^2 + b^2 - 2ab \cos(\alpha)} [/math]
Numeri complessi
Se definiamo
Un numero complesso ha un suo modulo, dato da
Esso può essere scritto anche in forma trigonometrica, cioè come
Per approfondimenti sui numeri complessi, vedi anche qua
Triangolo di Tartaglia
Nel triangolo di Tartaglia ogni numero è somma dei due numeri superiori e viene usato per
calcolare la potenza del binomio. Alla riga n+1 si ha la potenza n, ad es. alla riga 5 si ha il binomio
di potenza 4.
4 4 3 2 2 3 4
(a+b) = a + 4 a b + 6 a b + 4 a b + b
Coefficienti Binomiali
combinazioni di n elementi a gruppi di k
n n
!
C = =
n+1,k+1 ⋅ −
k
k ! (( n k )!
Es. combinazioni di n elementi a gruppi di k, ad es. il numero di combinazioni su 4 elementi a
gruppi di 2 è 6 e lo si vede facilmente dalla formula:
n 4 4
! 24
n
!
= = 6
dove n è uguale a 4 e 4 è uguale a 2
= =
⋅ ⋅
⋅ −
k 2
2
! (( 2 )! 2 2
k ! (( n k )!
Con la formula delle Combinazioni n elementi a gruppi di k è possibile calcolare anche le
probabilità di fare 6 al super enalotto
n n
!
= dove n è 90 e k è 6 (ovvero la sestina vincente):
⋅ −
k
k ! (( n k )! 1,4857E+138
= 622.614.630
90 90
!
= 720 3,3142E+126
=
⋅
6
6
! (
84 )!
circa 622 milioni di combinazioni, pertanto la probabilità di vincere : 1 diviso 622 milioni circa.
è chiamato , e vuol dire:
n! n fattoriale
= ⋅ − ⋅ − ⋅ ⋅ ⋅ ⋅
n n n n
! ( 1
) ( 2 ) ... 3 2 1
Il fattoriale di 0 è 1 (per convenzione), il fattoriale di 1 è 1. 9
= ⋅ −
Alta Proprietà del fattoriale è che n
! n ( n 1
)! dal momento che il fattoriale è una definizione
ricorsiva.
I numeri del triangolo di Tartaglia no detti anche Coefficienti Binomiali, particolarmente studiati
nell'ambito del calcolo combinatorio: si dimostra infatti che l'elemento di posizione k sulla riga n
del triangolo di Tartaglia è il numero di combinazioni di n-1 elementi di classe k-1:
Pertanto, la potenza del binomio può essere scritta anche con la formula seguente, che dobbiamo a
detta formula del Binomio di Newton:
n n
∑ −
⋅ ⋅
+ = k
n n k
( a b ) a b
k
=
k 0
Sistemi di Equazioni di Secondo Grado
Un sistema di Equazioni è un insieme di più equazioni che devono essere verificate
contemporaneamente, perciò le soluzioni dovranno essere l’intersezioni delle soluzioni delle
equazioni del sistema.
Un sistema di 2 equazioni può risolvere 2 incognite, uno di 3 equazioni può risolvere 3 incognite e
così via.
Dal punto di vista geometrico mediante la risoluzioni dei sistemi si trovano i punti di intersezioni
fra curve.
Ad esempio per trovare il punto di intersezione di 2 rette si mettono a sistema le 2 equazioni di
primo grado e si determinano le coordinate del punto di intersezione.
Altrimenti si possono trovare i punti di intersezioni di altre curve con una retta. Ad es: qui si ha
intersezione di retta con una circonferenza nel piano cartesiano.
+ =
2 2 1
x y
⋅ + ⋅ =
2 4 0
x y
A volte prima di iniziare la risoluzione del sistema è opportuno definire l’insieme di definizione. Ad
es. se ci stanno dei denominatori bisogna imporre che siano diversi da 0 (dal momento che un
numero diviso 0 dà un risultato infinitamente grande), oppure se vi è un radice di indice pari
bisogna accertarsi che il radicando sia maggiore o uguale a zero, o se si ha un log bisogna accertarsi
che l’argomento sia positivo 10
Metodi di Risoluzione
Fra i metodi di Risoluzione abbiamo:
Metodo di Sostituzione
Metodo del Confronto
Metodo di Riduzione
Regola di Cramer
Il è quello che si usa nella stragrande maggioranza dei casi e consiste
Metodo di sostituzione
nell’esplicitare un'incognita esprimendola in funzione delle altre, in una delle equazioni del sistema
e si sostituisce l'espressione così ottenuta nelle altre equazioni in luogo dell'incognita
corrispondente.
In questo modo l’incognita sparisce da tutte le equazioni eccetto la prima. Si applica iterativamente
il metodo fino a giungere ad una equazione con una sola incognita; si calcola il valore di
quest'ultima e si risale fino alla prima esplicitando via via i valori delle incognite calcolate. 11
Distanza fra due punti
La Distanza (euclidea) del punto A di coordinate (X ; Y ) dal B di coordinate (X ; Y ) è:
A A B B
( ) ( )
2 2
= − + −
d X X Y Y
,
A B B A B A
Se sia il punto A sia il si trovano su uno degli assi si può usare una formula semplificata.
Ad es. A e B sull’asse X, vuol dire che A ha coordinate (X ; 0) e B ha coordinate (X ; 0) è:
A B
= −
d X X
A , B B A
Ad es. A e B sull’asse Y, vuol dire che A ha coordinate (0; Y ) e B ha coordinate (0; Y ) è:
A B
= −
d Y Y
A , B B A
Equazione della Retta scritta in forma implicita
Una retta nel piano cartesiano è descritta in forma implicita dalla seguente equazione lineare:
a x + b y + c = 0
con a, b, c numeri reali e a, b non contemporaneamente nulli.
Per disegnare facilmente una retta in una piano (dal momento che per due punti passa una ed una
sola retta), basta trovare i due punti di intersezione con gli assi, ovvero basta risolvere i due sistemi
si equazioni sia con l’asse x (per trovare il punto di intersezione con l’asse x, y=0) sia con l’asse y
(per trovare il punto di intersezione con l’asse x)
⋅ + ⋅ + =
a x b y c 0
=
y 0
e per trovare il punto di intersezione con l’asse y (x=0), risolvere il seguente sistema
⋅ + ⋅ + =
a x b y c 0
=
x 0
Trovati i due punti che rappresentano le intersezioni con gli assi cartesiani possiamo disegnare la
retta, che passa da questi due punti.
Equazione della Retta scritta in forma esplicita
Una retta nel piano cartesiano è descritta in forma esplicita dalla seguente equazione lineare:
y = m x + q
dove m rappresenta il coefficiente angolare che tiene conto della pendenza della retta rispetto
all’asse x (ovvero l’angolo rispetto all’asse x);
e q rappresenta l’intercetta sull’asse y, ovvero il punto di intersezione della retta sull’asse y. 12
Per disegnare facilmente una retta in una piano basta trovare i punti di intersezione con gli assi.
Nella retta i forma esplicita già abbiamo il punto di intersezione con l’asse y, che avrà coordinate
(0, q), dal momento che q è l’intercetta dell’asse y.
Per trovare il punto di intersezione con l’asse x basta risolvere il seguente sistema:
= ⋅ +
y m x q
=
y 0
Coefficiente Angolare di una retta passante per due punti
Dati due punti P (X0; Y0) e Q (X1; Y1), il coefficiente della retta passante per questi due punti è:
−
y y
= 1 0
m −
x x
1 0
Passaggio dalla retta scritta in forma implicita alla retta scritta
in forma esplicita
Un equazione scritta in forma implicita si può trasformare in forma esplicita con dei semplici
passaggi matematici.
⋅ + ⋅ + = 0
a x b y c
⋅ = − ⋅ −
b y a x c
c
a
= − ⋅ −
x
y b
b
ponendo
a
= −
m b
c
= −
q b
Si ha l’equazione della retta in forma esplicita:
y = m x + q
Distanza di un punto da una retta
Data la retta r in forma implicita:
a x + b y + c = 0
La distanza di un punto P di coordinate P (X0; Y0) dalla r, è data dalla formula:
⋅ + ⋅ +
a X b Y c
= 0 0
d P r
, +
2 2
a b
Data la retta r in forma esplicita: 13
y = m x + q
La distanza di un punto P di coordinate P (X0; Y0) dalla r, è data dalla formula:
− ⋅ −
Y m X q
= 0 0
d P r
, + 2
1 m
Distanza di un punto da un piano
Nello spazio, la distanza di un punto da un piano si misura lungo la retta passante per il punto che
interseca perpendicolarmente il piano. In un sistema di coordinate tridimensionali ortogonali, date le
coordinare del punto P = (X , Y , Z )
0 0 0 0
L'equazione del piano p: ax + by + cz + d = 0
dal piano p è data dalla formula:
La distanza del Punto P 0
⋅ + ⋅ + ⋅ +
a X b Y c Z d
= 0 0 0
d P p
, + +
0 2 2 2
a b c
Fascio di Rette proprio
Un fascio di rette di dice proprio se tutte le rette che lo compongono passano per un punto detto
centro o sostegno del fascio. Questo punto può essere individuato come l’intersezione di due rette
qualsiasi del fascio.
Un fascio di rette proprio viene descritto in maniera simile ad una retta in forma esplicita, con la
che dipendono (o meglio sono paremtrizzate) da un parametro k che
differenza che sia m q
corrisponde ad una retta del fascio.
Le rette del fascio perciò si descrivono come:
y = m (k) x + q (k)
Tutte le rette del fascio proprio, ad eccezione della retta verticale di equazione x=x possono essere
0
parametrizzate da facendo dipendere m e q dal parametro k
; Y ), l’equazione del fascio può essere scritta:
Se il Centro del fascio ha coordinate C (X
0 0
− = ⋅ −
y Y m ( k ) ( x X )
0 0
Dove il coefficiente angolare varia al variare del parametro k.
Es. di fascio proprio con centro nell’origine 14
Fascio di Rette improprio
Un fascio di rette si dice se le sue rette sono tutte parallele tra loro. Come per il caso del
improprio
fascio proprio, tutte le rette di un fascio improprio possono essere parametrizzate per un parametro
k.
Stavolta però il coefficiente angolare delle rette del fascio è costante, ovvero m non cambia (infatti
non è parametrizzato da k).
Il fascio di rette può essere parametrizzato come
y = m x + q (k)
Condizione di Parallelismo
Due rette si dicono parallele se hanno lo stesso coefficiente angolare.
Es.
Date le due rette
r : y = m x + q
1 1 1
r y = m x + q
2 2 2
le rette r ed r sono parallele se m = m
1 2 1 2
Condizione di Perpendicolarità
Due rette si dicono perpendicolari se il coefficiente angolare di una retta è l’inverso del reciproco
dell’altra.
Es.
Date le due rette
r1: y = m x + q
1 1
r2 y = m x + q
2 2 15
1
= −
m
Le rette r ed r sono perpendicolari se:
1 2 1 m 2
Criteri di Similitudine
Primo Criterio di Similitudine fra Triangoli
Due triangoli sono simili se hanno due angoli ordinatamente congruenti (uguali), perciò anche il
terzo angolo sarà uguale
Secondo Criterio di Similitudine fra Triangoli
Due triangoli sono simili se hanno due lati ordinatamente proporzionali e gli angoli compresi
congruenti (uguali)
Terzo Criterio di Similitudine fra Triangoli
Due triangoli sono simili se hanno i tre lati ordinatamente proporzionali
Teorema di Talete
Un fascio di rette parallele determina sopra due trasversali due classi di segmenti direttamente
proporzionali
I pratica prese tre rette parallele a, b, c che tagliano due rette trasversali e nei punti A B C A’ B’
C’ allora si ha che il rapporto tra i segmenti omologhi dell’una e dell’altra retta è sempre costante.
Inoltre se presi AC e A'C', segmenti omologhi, si ha tra loro lo stesso rapporto di AB con A’B’ e di
BC con B'C', ovvero
Queste relazioni permettono di trovare la lunghezza di uno qualsiasi dei segmenti della quaterna, a
patto di averne almeno uno della stessa retta trasversale e due dell'altra, o la loro somma. 16
Ovviamente queste relazioni valgono presa qualsiasi coppia di segmenti omologhi.
Disequazioni di Secondo Grado
Una disequazione di secondo grado è un’espressione del tipo:
2
a x + b x + c > 0
Al posto del segno di maggiore ci può essere maggiore uguale, ed in quest’ultimo caso vuol dire che
sono comprese anche le soluzioni dell’equazione associata.
Oppure può essere del tipo:
2
a x + b x + c < 0
Al posto del segno di minore ci può essere minore uguale, ed in quest’ultimo caso vuol dire che
sono comprese anche le soluzioni dell’equazione associata
Per lo svolgimento si procede determinando le soluzioni dell’equazione associata di secondo grado,
pertando si calcola il delta e poi si determinano x ed x .
1 2
∆ = 2
b – 4 (a c)
− ± ∆
b
=
x
1
, 2 ⋅
2 a
A seconda del:
• Segno di a
• Del verso della disequazione
• Del segno del delta
Si usano i seguenti schemi risolutivi. 17
Se a è negativo le situazioni si invertono… ad ogni caso si può rendere positivo moltiplicando ambo
i membri per -1 e cambiando il verso della disequazione.
Nota: quando si moltiplicano ambo i membri per un numero negativo (es. -1), bisogna
.
cambiare il verso della disequazione
Sistemi di Disequazioni di Secondo Grado
Un sistema di Disequazioni è un insieme di più disequazioni che devono essere verificate
contemporaneamente, perciò le soluzioni dovranno essere l’intersezioni delle soluzioni delle
equazioni del sistema.
Può anche avvenire che le soluzioni delle varia disequazioni del sistema siano insiemi disgiunti e
perciò il sistema non avrà soluzioni, o meglio l’insieme soluzione è l’insieme vuoto.








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









