In questo appunto verranno descritti i concetti relativi al criterio di similitudine dei triangoli e tutto ciò che ne concerne in merito e alla loro applicazione nel caso di problema inerente ad un trapezio.
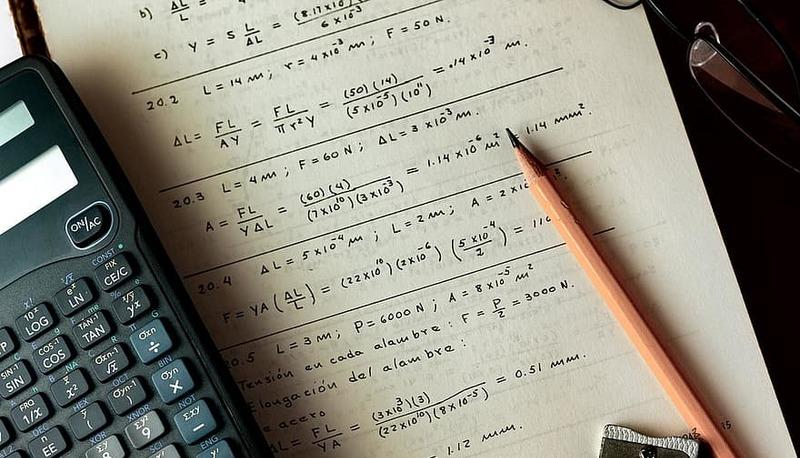
Indice
Cenni sui triangoli
Il triangolo è una figura piana che possiede tre lati e tre angoli. Il triangolo può essere classificato in base ai suoi lati e ai suoi angoli che lo compongono. La classificazione è la seguente riportata:- Triangolo Equilatero: tutti e tre i lati sono uguali e tutti e tre gli angoli sono anche uguali;
- Triangolo Isoscele: due lati su tre sono uguali e due angoli su tre sono uguali anch'essi
- Triangolo Scaleno: tutti e tre i lati sono diversi così come lo saranno anche gli angoli tra di loro
Condizioni di Similitudine
In geometria esistono tre criteri fondamentali utilizzati nella risoluzione di problemi di geometria base ed avanzati. I criteri di cui si è accennato sono i cosiddetti Criteri di Similitudine dei Triangoli. I criteri di similitudine permettono di stabilire se due triangoli risultino simili tra di loro se e solo se però rispettano le condizioni necessarie alla similitudine tra le due figure. Affinché due triangoli vengano identificati come triangoli simili devono valere le seguenti due condizioni di cui riportate di seguito:
- I tre angoli che compongono i due diversi triangoli devono risultare ordinatamente congruenti;
- I tre lati che compongono i due diversi triangoli devono risultare proporzionali tra di loro.
Per quanto riguarda la seconda condizione, è necessario ricordare il concetto di grandezze proporzionali tra di loro. Nel caso seguente, la proporzionalità che deve esistere tra i lati dei triangoli sta a significare che il rapporto tra i lati corrispondenti tra i due triangoli deve essere sempre un valore costante. Il valore costante di proporzionalità tra i lati prende il nome di Rapporto di Similitudine.
I tre criteri di similitudine dei triangoli
Dopo aver identificato le condizioni di similitudine, si può procedere ad individuare i tre criteri fondamentali di similitudine. Gli enunciati dei tre criteri di similitudine sono i seguenti di cui riportati:
- Primo criterio di similitudine: due triangoli sono definiti come triangoli simili se e solo se presentano i loro tre angoli rispettivamente congruenti tra di loro. Ciò significa dire che i due triangolo sono simili se possiedono anche solo due angoli congruenti.
- Secondo criterio di similitudine: due triangoli sono definiti come triangoli simili se e solo se presentano una coppia di lati che risultino proporzionali tra di loro e che l'angolo che risulta essere compreso tra i due lati debba essere anche congruente con quello del secondo triangolo;
- Terzo criterio di similitudine:due triangoli sono definiti come triangoli simili se e solo se presentano tutti e tre i lati che risultino ordinatamente proporzionali.
Proprietà dei triangoli simili
I triangoli che risultano essere simili tra possiedo delle particolari proprietà che sono il risultato delle delle stesse definizioni. Le proprietà sono le seguenti:
- Si osserva che se due triangoli sono simili il rapporto tra le altezze dei due triangoli debba risultare uguale al rapporto tra i lati stessi;
- Si osserva che se se triangoli sono simili il rapporto tra i perimetri dei due triangoli debba risultare anche uguale al rapporto tra i lati stessi;
- Si osserva che se due triangoli sono simili il rapporto tra le aree dei due triangoli debba risultare anche uguale al rapporto tra i lati stessi.
Problema sul trapezio: risoluzione attraverso il criterio della similitudine tra triangoli
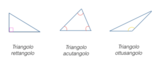
Si consideri il seguente problema di geometria su un trapezio, e si decida di risolvere il problema attraverso il criterio di similitudine dei triangoli.Si consideri un trapezio scaleno. Del trapezio considerato sono note le misure di tutti i suoi lati che lo compongono, ovvero delle due sue basi e dei due suoi lati obliqui. Prolungando i lati obliqui del trapezio si osserva come sia possibile andare a costruire un triangolo (di cui vertici
Dalle nozioni geometriche, è noto che il lato di un triangolo risulti essere la base maggiore del trapezio iniziale, gli altri due lati, invece, risultano essere formati dai lati obliqui del quadrilatero con i relativi prolungamenti, ovvero pari a
Le incognite richieste dal problema sono i prolungamenti dei due lati obliqui del trapezio. Il problema di cui oggetto di discussione è possibile osservarlo graficamente nella presente immagine riportata di seguito.

Osservando la figura, si prendano in considerazione i triangoli
Gli angoli dei triangoli considerati di
Sia nota la misura delle due basi del trapezio quindi si è a conoscenza del rapporto di similitudine tra i lati dei due triangoli. Si osserva che il rapporto vale rispettivamente pari a
Per determinare la lunghezza del lato
Da qui, la proporzione risolta fornisce la misura del prolungamento
Infine risulta che il lato AE misura:
Scriviamo ora una proporzione analoga per determinare la lunghezza del lato CE.
Da qui, la proporzione risoltafornisce la misura del prolungamento
Infine risulta che il lato BE misura:
A questo punto non ci resta che sommare i tre lati per determinare la misura del perimetro.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo