Cosa sono i numeri primi: definizioni e criteri

In quest'appunto troverai delle definizioni e dei criteri fondamentali riguardanti i numeri primi.

La definizione di un numero primo

Si definiscono numeri primi i numeri intero positivi che hanno per divisori soltanto se stessi e il numero

.
Per esempio, si ha che:

• [math]5[/math]
  risulta essere numero primo perché ha come unici divisori
  [math]5[/math]
  e
  [math]1[/math]
• [math]8[/math]
  non è numero primo in quanto è divisibile per
  [math]1[/math]
  ,
  [math]2[/math]
  ,
  [math]4[/math]
  e
  [math]8[/math]

L'importanza della definizione di numero primo, che a volte sembra poco significativa, si riscontra nel Teorema fondamentale dell'Aritmetica.

Ogni numero naturale maggiore di

si scrive in modo unico, a meno dell'ordine, come prodotto di numeri primi.

Questo è ciò che si utilizza quando scomponiamo i numeri in fattori primi per la determinazione del MCD (Massimo Comune Divisore) o del mcm (minimo comune multiplo). Il Massimo Comune Divisore rappresenta il più grande tra i divisori in comune tra due numeri. Il massimo comune divisore tra i numeri

e

è

poiché essi sono rispettivamente componibili in:

.

Il minimo comune multiplo è invece il più piccolo multiplo in comune tra i due numeri. Per calcolarlo è opportuno moltiplicare ai fattori non comuni il fattore comune elevato all'esponente massimo con cui compare. In questo caso vi è un solo fattore non comune (

) e il fattore comune

compare al massimo con esponente

. Per questo motivo il minimo comune multiplo tra

e

è

.

La quantificazione dei numeri primi con dimostrazione e la tabella dei numeri primi

I numeri primi sono infiniti. Per questo motivo, per valutare se un numero sia o meno primo è opportuno consultare la tabella dei numeri primi: essa consiste nell'elenco di tutti i numeri primi all'interno di un dato range.
E' possibile dimostrare l'infinità dei numeri primi considerando diverse strategie: vediamo quella di Euclide, la più antica giunta sino a noi.

Dimostrazione di Euclide sui numeri primi

La dimostrazione di Euclide si basa su un ragionamento per assurdo, ossia partendo da un ipotesi opposta rispetto alla tesi da dimostrare. Questo comporta il raggiungimento di conseguenze contraddittorie, le quali dimostrano che l'ipotesi imposta sia falsa e che la tesi opposta sia veritiera.

Supponiamo che esistano

:

Calcoliamone il prodotto:

.
Consideriamo a questo punto il valore:

Questo numero non sarà divisibile per nessuno degli

, il resto delle divisioni sarà sempre

. Questo vuol dire che il nuovo numero

, essendo diverso da

, sarà a sua volta primo.
Abbiamo ottenuto un assurdo, questo vuol dire che l'ipotesi iniziale è sbagliata. Quindi i numeri primi sono infiniti.

I criteri per valutare i numeri primi

Facilmente si può notare che tutti i numeri pari, eccetto

, non sono primi, in quanto divisibili per

.

Lo stesso ragionamento vale per i criteri di divisibilità che conosciamo. Sicuramente non sono primi i numeri che soddisfano i principali criteri di divisibilità, come quelli cui somma delle cui cifre sia multiplo di tre o di nove (divisibilità per

) o che termini con zero oppure cinque (divisibilità per

e per

).
Un altro criterio interessante riguarda la divisibilità per

: un numero risulta infatti essere divisibile per

se sottraendo alla somma di tutte le cifre di posizione pari tutte quelle in posizione dispari si ottiene un valore nullo o un numero multiplo di

(divisibilità per

).

Esistono però alcuni risultati per stabilire se un numero, indipendentemente dalla sua grandezza, sia primo o meno:

• Test di Fermat:
in realtà questo test ci dice quando un numero
[math]n[/math]
non è un numero primo.
• Test di Wilson:
  
  sono dei test di probabilità che valgono solo per alcune categorie di numeri primi, come il Test di Lucas-Lehmer per i numeri primi di Mersenne
• Test di primalità statistici come l'Algoritmo di Miller-Rabin

La risposta è NO.
Per rendersi conto della motivazione di questa risposta basta considerare il già citato Teorema Fondamentale dell'Aritmetica: ogni numero naturale maggiore di 1 si scrive in modo unico, a meno dell'ordine, come prodotto di numeri primi.
Se

fosse un numero primo, avremmo questa situazione:

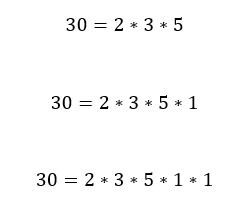
E potremmo continuare con un numero arbitrario di

. Questo significa che, anche a meno dell'ordine, la fattorizzazione non sarebbe unica.

Per ulteriori approfondimenti sui numeri primi vedi anche qui