Le equazioni di primo grado
Le equazioni di primo grado sono equazioni polinomiali di grado uno, e possono essere risolte seguendo una serie di passaggi e regole. Ecco una mappa concettuale che illustra tutti gli step e le regole per risolvere un'equazione di primo grado:Step 1: Isolare il Termine con la Variabile
1.1. Inizia osservando l'equazione e identifica il termine che contiene la variabile (solitamente indicato come "x").
1.2. Se ci sono termini senza variabili, spostali dal lato opposto dell'uguale rispetto al termine con la variabile.
Step 2: Semplificare l'Equazione
2.1. Semplifica entrambi i lati dell'equazione eseguendo le operazioni matematiche (addizione, sottrazione, moltiplicazione, divisione) necessarie per ridurre l'equazione al suo minimo comune denominatore.
Step 3: Isolare la Variabile
3.1. Per isolare la variabile, esegui l'operazione inversa presente nel termine con la variabile. Ad esempio, se hai "2x", esegui la divisione per "2" per ottenere "x".
Step 4: Verifica
4.1. Per assicurarti di aver trovato la soluzione corretta, sostituisci il valore della variabile (x) nell'equazione originale e verifica se entrambi i lati sono uguali. Se lo sono, hai trovato la soluzione corretta.
Regole Importanti:
Ricorda sempre che qualsiasi operazione eseguita su un lato dell'equazione deve essere eseguita anche sul lato opposto per mantenere l'equilibrio dell'equazione.
Se moltiplichi o dividi entrambi i lati dell'equazione per un numero diverso da zero, l'uguaglianza rimarrà valida.
Se sommi o sottrai la stessa quantità da entrambi i lati, l'uguaglianza rimarrà valida.
Se moltiplichi o dividi entrambi i lati dell'equazione per zero, dovrai prestare attenzione a possibili eccezioni.
Casi Particolari:
Equazione senza Soluzione: Se risolvi l'equazione e arrivi a un'affermazione del tipo "0 = 5" o "3 = 3", significa che l'equazione non ha soluzione.
Equazione con Infinite Soluzioni: Se risolvi l'equazione e arrivi a un'affermazione del tipo "0 = 0", significa che l'equazione ha infinite soluzioni, ovvero è vera per qualsiasi valore della variabile.
Esempi:
Equazione: 3x + 5 = 11
Step 1: Isola la variabile: 3x = 11 - 5 → 3x = 6
Step 2: Semplifica: x = 6 / 3 → x = 2
Step 4: Verifica: 3(2) + 5 = 6 + 5 = 11 (corretto)
Equazione: 2(x - 3) = 8
Step 1: Isola la variabile: 2(x - 3) = 8 → x - 3 = 8 / 2 → x - 3 = 4
Step 2: Semplifica: x = 4 + 3 → x = 7
Step 4: Verifica: 2(7 - 3) = 2(4) = 8 (corretto)
Equazione: 2x + 4 = 2x - 1
Step 1: Isola la variabile: 2x - 2x + 4 = -1 → 4 = -1 (senza soluzione)
Equazione: 3x = 3x
Step 1: Isola la variabile: 3x - 3x = 0
Step 4: Verifica: 0 = 0 (infinitamente vera)
Ora hai una mappa concettuale completa che ti guiderà attraverso la risoluzione delle equazioni di primo grado, insieme a regole e esempi chiave. Ricorda sempre di applicare le operazioni in modo accurato e di verificare le tue soluzioni per garantire la correttezza.
In breve, la risoluzione di equazioni di primo grado coinvolge una serie di passaggi e regole chiave:
Isolamento del termine con la variabile.
Semplificazione dell'equazione eseguendo operazioni matematiche.
Isolamento della variabile attraverso l'operazione inversa del termine.
Verifica della soluzione sostituendo il valore della variabile nell'equazione originale.
Importante è mantenere l'equilibrio dell'equazione applicando le stesse operazioni su entrambi i lati. In alcuni casi, si possono ottenere equazioni senza soluzione o con infinite soluzioni. Gli esempi illustrano questi concetti nella pratica. La comprensione di queste regole è essenziale per la risoluzione efficace di equazioni di primo grado.
ATTENZIONE RICORDATI DI SEGUIRE CIO' CHE IL TUO PROFESSORE DICE E DI PRESTARE ASCOLTO A COME VUOLE SCRITTE LE RISOLUZIONI.
Domande da interrogazione
- Quali sono le equazioni di primo grado?
- Quali sono i passaggi per risolvere un'equazione di primo grado?
- Quali sono le regole importanti da seguire nella risoluzione di equazioni di primo grado?
- Cosa significa se un'equazione di primo grado ha una soluzione del tipo "0 = 5"?
- Cosa significa se un'equazione di primo grado ha una soluzione del tipo "0 = 0"?
Le equazioni di primo grado sono equazioni polinomiali di grado uno.
I passaggi per risolvere un'equazione di primo grado sono: isolare il termine con la variabile, semplificare l'equazione, isolare la variabile e verificare la soluzione.
Le regole importanti da seguire nella risoluzione di equazioni di primo grado sono: mantenere l'equilibrio dell'equazione applicando le stesse operazioni su entrambi i lati, moltiplicare o dividere entrambi i lati per un numero diverso da zero mantiene l'uguaglianza, sommare o sottrarre la stessa quantità da entrambi i lati mantiene l'uguaglianza e prestare attenzione a possibili eccezioni quando si moltiplica o divide entrambi i lati per zero.
Se un'equazione di primo grado ha una soluzione del tipo "0 = 5", significa che l'equazione non ha soluzione.
Se un'equazione di primo grado ha una soluzione del tipo "0 = 0", significa che l'equazione ha infinite soluzioni, ovvero è vera per qualsiasi valore della variabile.

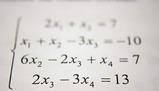





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo