Numeri complessi: Risolvere la seguente equazione con numeri complessi: (iz)^3 = z * \bar{z}

di _stan

Ominide

5 min. di lettura

Vota

Per risolvere un'equazione di questo tipo dobbiamo procedere considerando la rappresentazione esponenziale dei numeri complessi.
Un numero complesso

[math]z[/math]

può essere scritto in questo modo:

[math] z = \>br /> ho e^{i \theta}[/math]

dove

[math]\>br /> ho[/math]

rappresenta il modulo di

[math]z[/math]

, mentre

[math]\theta[/math]

è un angolo che rappresenta l'argomento del numero complesso.
L'angolo

[math]\theta[/math]

servirà per determinare la posizione delle soluzioni sulla circonferenza goniometrica; ricordiamo, infatti, che vale la seguente uguaglianza:

[math] e^{i \theta} = \\cos(\theta) + i \\sin (\theta) [/math]

Vediamo, quindi, come esprimere in forma esponenziale tutti i termini della nostra equazione.

[math] (iz)^3 = i^3 \cdot z^3 [/math]

Iniziamo dal termine

[math]i^3[/math]

; dalla relazione fondamentale si ha che

[math]i^2 = -1[/math]

, quindi:

[math]i^3 = i^2 \cdot i = - i [/math]

Tale numero complesso può essere rappresentato da

[math] e^{ 3/2 π i}[/math]

, infatti:

[math] e^{ i 3/2 π} = \\cos(3/2 π) + i \\sin (3/2 π) = - i [/math]

Mentre il termine

[math] z^3[/math]

può essere rappresentato come:

[math] z^3= (\>br /> ho e^{i \theta})^3 = \>br /> ho^3 e^{ i 3\theta} [/math]

Ora consideriamo i termini

[math]z[/math]

[math]\bar{z}[/math]

; possiamo esprimere i due termini nel seguente modo:

[math] z = \>br /> ho e^{i \theta} , \bar{z} = \>br /> ho e^{ -i \theta}[/math]

In quanto se

[math]z[/math]

è espresso da:

[math] e^{i \theta} = \\cos(\theta) + i \\sin (\theta) [/math]

necessariamente il suo coniugato sarà:

[math] \\cos(\theta) - i \\sin (\theta) = e^{ - i \theta} [/math]

Torniamo ora alla nostra equazione e scriviamo tutti i termini in forma esponenziale:

[math] e^{ 3/2 π i} \cdot \>br /> ho^3 e^{ i 3\theta} = \>br /> ho e^{i \theta} \cdot \>br /> ho e^{- i \theta} [/math]

Svolgiamo i prodotti al primo e al secondo membro:

[math] \>br /> ho^3 \cdot e^{ 3/2 π i + i 3\theta} = \>br /> ho^2 \cdot e^{i \theta - i \theta} [/math]

Da cui si ottiene:

[math] \>br /> ho^3 \cdot e^{ i (3/2 π + 3\theta)} = \>br /> ho^2 [/math]

Da questa relazione, procediamo impostando un sistema che rappresenta le condizioni che devono essere verificate per ottenere l'uguaglianza:

[math] \begin{cases} & ( \>br /> ho^3 = \>br /> ho^2 \\ e^{ i (3/2 π + 3\theta)} = e^0 = 1 \ \end{cases} [/math]

Nella risoluzione dell'equazione dobbiamo tener conto del fatto che, poiché l'esponente di

[math]z[/math]

massimo è 3, quindi avremo esattamente tre soluzioni.

Dalla prima equazione risulta evidente che deve essere

[math] ro = 1 V \>br /> ho = 0[/math]

.
Risolviamo ora la seconda equazione; ricordiamo che sonho validi tutti gli angoli

[math]\theta[/math]

multipli di

[math]360°[/math]

[math] e^{ i (3/2 π + 3\theta)} = e^0 \to 3/2 π + 3\theta = 2kπ [/math]

Quindi:

[math] 3\theta = 2kπ - 3/2 π \to \theta = frac(2kπ - 3/2 π)(3) [/math]

[math] \theta = frac(4kπ - 3π)(6) [/math]

Dato che dobbiamo ottenere esattamente tre soluzioni, i valori che può assumere il coefficiente

[math]k[/math]

sono

[math] 0, 1, 2[/math]

.
Determiniamo i tre angoli che individuano le tre soluzioni dell'equazione:

[math] k = 0 \to \theta = -π/2 [/math]

[math] k = 1 \to \theta = frac(π)(6) [/math]

[math] k = 2 \to \theta = frac(5π)(6) [/math]

Ora dobbiamo scrivere i numeri complessi

[math] z_1[/math]

[math] z_2[/math]

[math] z_3[/math]

nella forma

[math] a + ib[/math]

.
Per farlo, ricorriamo alla rappresentazione trigonometrica dei numeri complessi, ovvero sfruttiamo l'uguaglianza:

[math] z = e^{i \theta} = \\cos(\theta) + i \\sin (\theta) [/math]

Nel primo caso abbiamo:

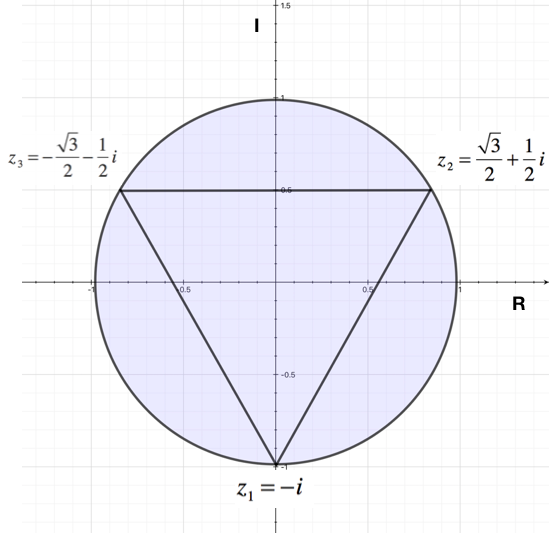
[math] z_1 = \\cos(-π/2) + i \\sin (-π/2) = - i [/math]

Nel secondo caso:

[math] z_2 = \\cos(π/6) + i \\sin (π/6) = frac(\sqrt3){2} + frac(1){2} i [/math]

Nel terzo caso:

[math] z_3 = \\cos(5π/6) + i \\sin (5π/6) = - frac(\sqrt3){2} + frac(1){2} i [/math]

Nel caso

[math]\>br /> ho=0[/math]

abbiamo la soluzione nulla, ovvero

[math]z=0[/math]

Come possiamo notare, le soluzioni sono tutte e quattro complesse, a due a due coniugate; rappresentando le soluzioni ottenute su una circonferenza goniometrica possiamo notare che esse individuano i vertici di un triangolo equilatero.

Numeri complessi: Risolvere la seguente equazione con numeri complessi: (iz)^3 = z * \bar{z}

Per risolvere un'equazione di questo tipo dobbiamo procedere considerando la rappresentazione esponenziale dei numeri complessi. Un numero complesso z può essere scritto in questo modo: z = rho...

Potrebbe interessarti anche

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Potrebbe interessarti anche

Appunti correlati

Numeri complessi: Risolvere la seguente equazione con numeri complessi: z^3 = 1

Risolvere la seguente equazione con numeri complessi: z^4 = 1

Numeri complessi: Risolvere la seguente equazione con numeri complessi: [math] z^2 - 3iz - 2 = 0 [/math]

Numeri complessi: Risolvere la seguente equazione con numeri complessi: [math] z^2 = ( \bar{z})^2 * \Big(4 (|z|)^2 - 1 \Big) [/math]

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.