Concetti Chiave
- A box weighing 500N is suspended by a vertical rope connected to two other ropes forming angles of 30° and 60° with the horizontal.
- The task is to determine the tensions in each of the two oblique ropes supporting the box.
- A Cartesian reference system is used, with the vertical axis parallel to the box's weight force and the horizontal axis perpendicular to it.
- The equilibrium condition implies that the sum of forces along both the x-axis and y-axis is zero.
- Calculations show that the tension in one rope, T₁, is 250N, while the tension in the other rope, T₂, is 250√3 N.
Testo dell'esercizio
La figura mostra una cassa, di peso uguale a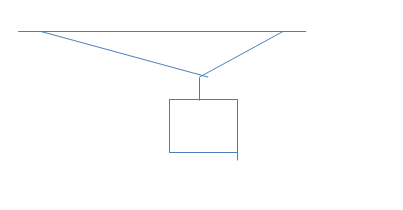[math]500N[/math]
, appesa a una corda verticale che, nel punto P, si congiunge con altre due corde fissate a un sostegno. Queste formano con l' orizzontale angoli di 30° e 60°. Determina quali sono le tensioni di ciascuna delle due corde oblique. 
Svolgimento dell'esercizio
Adottiamo un sistema di riferimento cartesiano in cui l'asse verticale è parallelo alla forza peso della cassa, mentre l'asse orizzontale passa perpendicolarmente ad essa.Chiamiamo
[math] T_1, T_2 [/math]
le due tensioni.Dal momento che la cassa è in equilibrio non ci aspettiamo che essa si muova, dunque la somma delle forze lungo l'asse x e lungo l'asse y è nulla.
Nel primo caso questa cosa è equivalente a:
[math] T_1 \cos(30°) = T_2 \cos(60°) \to \sqrt{3} T_1 = T_2 [/math]
Lungo l'asse y invece accade che:
[math] P = T_1 \sin (30 °) + T_2 \sin (60 °) = T_1 \sin (30 °) + \sqrt{3} T_1 \sin (60°) = 500 N [/math]
[math] T_1 = 250 N [/math]
risolvendo l'equazione. Ma allora [math] T_2 = 250 \sqrt{3} N [/math]
perché [math] \sqrt{3} T_1 = T_2 [/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
