Conservazione dell'energia e lavoro di una forza

Esercizio su energia meccanica e forza elastica: calcolo della compressione della molla urtata da un carrello in movimento soggetto a forza di attrito.

_francesca.ricci
di _francesca.ricci
Ominide
3 min. di lettura
Vota

Concetti Chiave

  • Il carrello arriva al punto B con un'energia meccanica di 39,2 J, calcolata tramite il teorema della conservazione dell'energia meccanica.
  • Nel tratto BC, il carrello subisce una perdita di energia di 30,2 J a causa della forza di attrito.
  • La forza di attrito nel tratto BC è determinata come 3,36 N, utilizzando il lavoro negativo svolto.
  • La molla viene compressa a seguito dell'energia finale del carrello, con una costante elastica di 1000 N/m.
  • La compressione della molla è determinata tramite il lavoro esercitato e risulta in una formula per calcolare la deformazione.

Di seguito andremo ad analizzare un esercizio svolto con tre punti in cui viene richiesto di calcolare, utilizzando nozioni teoriche sull'energia meccanica, diverse quantità.

Indice

  1. Testo dell'esercizio
  2. Svolgimento dell'esercizio (1)
  3. Svolgimento dell'esercizio (2)
  4. Svolgimento dell'esercizio (3)

Testo dell'esercizio

Il carrello della figura ha la massa di
[math]2 kg[/math]
e giunge nel punto
[math]A[/math]
con velocità trascurabile.
Nel tratto
[math]AB[/math]
non c'è attrito, nel tratto
[math]BC[/math]
, lungo
[math]9 m[/math]
, il carrello perde energia, perché agisce una forza di attrito costante. Il carrello arriva nel punto
[math]C[/math]
con velocità di
[math] 3 m/s[/math]
e comprime la molla che ha una costante elastica di
[math]1000 N/m[/math]
.
  • Con quale energia meccanica giunge nel punto
    [math]B[/math]
    ?
  • Quanto vale la forza di attrito nel tratto
    [math]BC[/math]
    ?
  • Di quanto si comprime la molla?
carrello_e_molla

Svolgimento dell'esercizio (1)

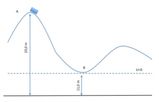
Secondo il teorema della conservazione dell'energia meccanica, l'energia meccanica nel punto
[math]A[/math]
è uguale a quella nel punto
[math]B[/math]
. Quindi calcoliamo l'energia meccanica nel punto
[math]A[/math]
sommando l'energie cinetica e quella potenziale di quel punto.

Poiché il carrello giunge nel punto

[math]A[/math]
con velocità trascurabile, la sua energia cinetica è nulla; l'energia potenziale, invece, è data dalla formula:

[math] U = mgh \to U_A = 2 kg \cdot 9,8 m/s^2 \cdot 2m = 39,2 J [/math]

Quindi:

[math] E_A = E_B = U_A = 39,2 J [/math]

Ponendo in modo arbitrario il livello zero di energia potenziale nel punto

[math]B[/math]
, sappiamo che l'energia meccanica in
[math]B[/math]
è uguale alla sola energia cinetica di quel punto, quindi:

[math] E_A = U_B + k_B = k_B = 39,2 J [/math]

Svolgimento dell'esercizio (2)

Per determinare la forza di attrito nel tratto
[math]BC[/math]
dobbiamo conoscere il lavoro esercitato dal carrello in quel tratto. Sappiamo che il lavoro è uguale alla variazione di energia cinetica, quindi:

[math] L = \Delta k = k_f - k_i = 1/2 m v_f ^2 - 1/2 m v_i ^2 [/math]

In particolare

[math] L _{BC}= \Delta k = k_C - k_B = 1/2 m v_C ^2 - 1/2 m v_B ^2 [/math]

Troviamo quindi il lavoro esercitato in quel tratto:

[math] L _{BC}= 1/2 \cdot 2 kg \cdot (3 m/s)^2 - 39,2 J = - 30,2 J [/math]

Notiamo che il lavoro nel tratto

[math]BC[/math]
è negativo, proprio perché agisce una forza di attrito. Sapendo che il lavoro è uguale allo spostamento, possiamo determinare la forza di attrito:

[math] L _{BC} = - F \cdot S \to F = - \frac{L_{BC}}{S} [/math]

[math] F = -\frac{L_{BC}}{S} = - \frac{- 30,2 J}{9m} = 3,36 N [/math]

Svolgimento dell'esercizio (3)

Il lavoro esercitato per comprimere la molla è dato dalla formula:

[math] L = \frac{1}{2} k x^2 [/math]

dove

[math]k[/math]
è la costante elastica e vale
[math]1000 N/m[/math]
, mentre
[math]x[/math]
è la lunghezza del tratto di compressione della molla. Troviamo quindi
[math]x[/math]
:

[math] L = 1/2 k x^2 \to x^2 = \frac{2L}{k} \to x = \sqrt{\frac{2L}{k}} [/math]

Domande da interrogazione

  1. Qual è l'energia meccanica del carrello nel punto B?

    2. L'energia meccanica nel punto B è uguale a quella nel punto A, che è 39,2 J, poiché nel tratto AB non c'è attrito.

  2. Come si calcola la forza di attrito nel tratto BC?

    3. La forza di attrito nel tratto BC si calcola utilizzando il lavoro esercitato dal carrello, che è -30,2 J, e la distanza di 9 m, risultando in una forza di attrito di 3,36 N.

  3. Qual è la velocità del carrello nel punto C?

    4. La velocità del carrello nel punto C è di 3 m/s.

  4. Di quanto si comprime la molla?

    5. La compressione della molla si calcola usando la formula del lavoro e la costante elastica di 1000 N/m, ma il testo non fornisce direttamente il valore di compressione.

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Vai al forum

I migliori insegnanti di Fisica

Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Matteo

Matteo S.

Supertutor
Verificato

Insegnante di Aiuto tesi, Algebra, Geometria, Matematica

a partire da 20 €/ora
most booked
Mostra altri Tutor