
L'esame di maturità del liceo scientifico è alle porte. E' bene, quindi, iniziarsi a preparare per affrontare al meglio la prova di matematica 2015. Può essere utile, perciò, dare uno sguardo alla risoluzione approssimata di equazioni, uno dei quesiti di matematica più frequenti. Il prof di matematica, Francesco Bologna, ci spiega come risolvere tale problema sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.
Scopri tutte le tracce della maturità scientifica degli anni passati
Impara ad usare la calcolatrice, guarda il nostro video!
Sappiamo che non è sempre possibile trovare le soluzioni di un'equazione con metodi algebrici (come per le equazioni di primo o secondo grado...), esistono infatti delle equazioni di grado superiore o trascendenti per le quali non ci sono formule risolutive, ma bisogna utilizzare procedimenti alternativi di risoluzione approssimata.
Solo durante l'ultimo anno del corso di studi il problema raggiunge la sua piena maturazione, quando si impara a rappresentare le equazioni graficamente, a separare le radici e poi ad applicare qualche tecnica numerica, utile per
ottenere almeno approssimativamente una radice: si tratta di un argomento classico che si sviluppa con le nozioni di calcolo infinitesimale.
Tale procedure si basano, in genere, su due fasi:
-
1. determinare gli intervalli in cui sono presenti le soluzioni.
-
2. calcolare la soluzione.
In genere le funzioni assegnate hanno per dominio un intervallo (anche non limitato) e sono continue e derivabili.
Le procedure si basano su due teoremi molto importanti:
-
1. Teorema dell' Esistenza degli Zeri.
-
2. Teoremi di unicità degli zeri.
Teorema dell'esistenza degli zeri.
Sia
una funzione continua in un intervallo chiuso e limitato
tale che
Allora esiste
Primo Teorema di unicità degli zeri.
Sia
una funzione continua in un intervallo chiuso e limitato
derivabile in
con derivata prima diversa da zero nell'intervallo,
tale che
Allora esiste ed unico un punto
Secondo Teorema di unicità degli zeri.
Sia
una funzione continua in un intervallo chiuso e limitato
derivabile due volte in
tale che
e
Allora esiste ed unico un punto
Dopo aver stabilito l'esistenza e l'unicità dovremo calcolare tale soluzioni. Esistono diversi procedimenti iterativi. Uno tra i più diffusi e studiati è il metodo di bisezione.
Si determina il punto medio
dell'intervallo
e si calcola il valore
della funzione in
I casi possibili sono tre:
in tal caso abbiamo determinato la soluzione;
ha lo stesso segno di a e ciò indurrà che la soluzione è nell'intervallo
ha lo stesso segno di b e ciò indurrà che la soluzione è nell'intervallo
Si riparte con il nuovo intervallo e si procede allo stesso modo, definendo il punto medio e calcolando la funzione in tale punto, al fine di escludere, ancora una volta, una metà dell'intervallo di lavoro. Dopo aver compiuto n passi, assumeremo come soluzione il valore medio n-esimo.
RISOLUZIONE DI EQUAZIONI CON METODI APPROSSIMATI
Esempio: Dimostrate che l'equazione
ammette una e una sola soluzione reale. Iniziamo con il verificare se l'equazione ammette soluzione applicando i teoremi sull'esistenza e l'unicità.
Calcoliamo il dominio della funzione.
Riscriviamo la funzione della forma
e tracciamo le due funzioni elementari al fine di individuare graficamente un intervallo di analisi
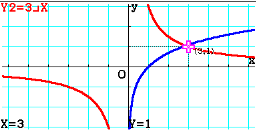
Scegliamo l'intervallo
Verifichiamo i teoremi su enunciati.
Verifichiamo che
Infatti
e
Calcoliamo la derivata prima della funzione:
Verifichiamo che essa è diversa da zero per ogni x appartenente all'intervallo.
Poniamo
x=e^{-1}=0.367[/math]
non appartenente ad
Calcoliamo per completezza la drivata seconda. Si verificherà facilmente che essa è sempre positiva in
Possiamo affermare che esiste ed unico un punto
:f\left(x_0\right)=0.[/math]
Calcoliamo il valore di
Calcoliamo
Per le considerazioni su fatte, consideriamo l'intervallo
e calcoliamo il punto medio
Calcoliamo il valore di
Calcoliamo
Per le considerazioni su fatte, consideriamo l'intervallo (2,25;3,125) e calcoliamo il punto medio
Calcoliamo il valore di
Calcoliamo
Per le considerazioni su fatte, consideriamo l'intervallo (2,68;3,125) e calcoliamo il punto medio
Calcoliamo il valore di
Così procedendo determineremo la soluzione cercata.
Vediamo come la calcolatrice può semplificarci la procedura.
Passaggio #1
Come abbiamo visto, il problema non è risolvibile per via elementare ma necessità dell'applicazione di alcuni teoremi di analisi (che dobbiamo indicare!!).
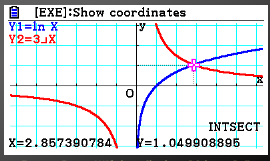
Possiamo però utilizzare la calcolatrice per determinare, la soluzione per via numerica in modo da finalizzare la procedura classica. Digita il tasto MODE e scegli l'opzione 1.

Passaggio #2
Trascrivi l'equazione utilizzando la funzione ALPHA
-scheda1.png)
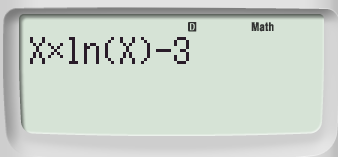
Passaggio #3
Digita il comando SOLVE, come seconda funzione del comando CALC.
-scheda1.png)
Comparirà la scritta SOLVE FOR X: digita 2 (o un altro valore intero!) e otterrai la soluzione cercata.
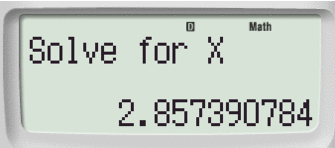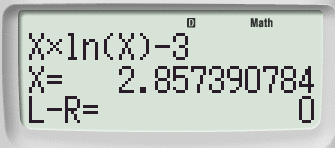
Passaggio #4
Una volta nota la soluzione possiamo scegliere l'intervallo più "adatto" e procedere nel modo classico.
E' utile osservare che per determinare il valore della funzione in un punto basta ripetere il Passaggio #2 e digitare il comando CALC.

La calcolatrice ci chiederà che valore sostituire ad
In tal modo potremo determinare rapidamente i valori della
funzione in
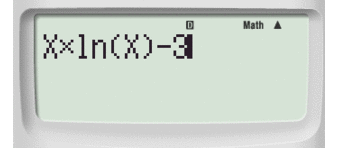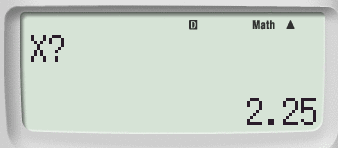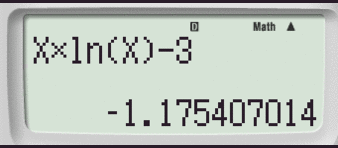






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo