Maturità 2018, lo studio della risoluzione approssimata di equazioni con la calcolatrice grafica

Lo studio della risoluzione di equazioni rappresenta un filo conduttore che accompagna gli studenti dei nostri licei per l’intero corso degli studi. Di volta in volta le equazioni sono presentate in una veste diversa scandendo, anno dopo anno, la progressione degli studi matematici e diventando, in questi ultimi anni sempre più spesso, tema presente agli Esami di Stato.

Risolvere un'equazione vuol dire determinare tutti i numeri reali

Questi numeri si chiamano soluzioni dell'equazione data o zeri della funzione, talvolta radici. Spesso l’insieme di definizione delle soluzioni si amplia aggiungendo anche quelle complesse.

L’espressione algebrica caratterizza la funzione. Se l’espressione analitica della funzione presenta solo operazioni di somma, sottrazione, moltiplicazione, potenza e radice, la f(x) e la corrispondente equazione si dicono algebriche; se nell’espressione analitica sono presenti funzioni trascendente, cioè composta per mezzo delle funzioni elementari esponenziale, logaritmo, seno, coseno, allora la funzione e la corrispondente equazione sono dette trascendenti.

Quando è possibile trovare con un metodo algebrico le soluzioni di una equazione si dice che esiste un metodo esatto di risoluzione. Esempi sono le equazioni di primo e secondo grado.

Tuttavia esistono diversi tipi di equazioni per le quali non esistono tecniche di risoluzione esatta; esempi sono le equazioni di grado superiore al quarto o alcune equazioni trascendenti.

Per quest’ultime dobbiamo quindi pensare a “metodi approssimati” che ci consentano di determinare, mediante un numero finito di operazioni elementari, le radici di un’equazione con un accettabile e valutabile grado di precisione.

Molti dei metodi approssimati di risoluzione numerica, elaborati da matematici illustri quali Newton, Fourier e Lagrange, sono basati sulla costruzione di successioni convergenti di numeri reali.
I termini di tale successione rappresentano valori approssimati della soluzione ottenuti mediante cicli di iterazioni successive.

Il computo dei termini della successione spesso è lungo e tedioso ed è quindi ovvio demandare alla calcolatrice i calcoli ricorsivi.

In questo paragrafo verranno prese in esame le risoluzioni di equazioni in cui le funzioni sono continue e più volte derivabili e si darà come prerequisito la conoscenza dei teoremi sulle funzioni continue (Rolle, Lagrange), del Teorema degli Zeri, dei Teoremi di unicità e del Teorema fondamentale dell'Algebra.

Le tecniche risolutive si svolgono in genere in due momenti:

1) Separazione delle radici e determinazione degli intervalli che contengono una ed una sola soluzione;

In questa prima fase si può riscrivere f(x) come differenza di due funzioni più semplici

e riprodurre l'equazione nella nuova forma:

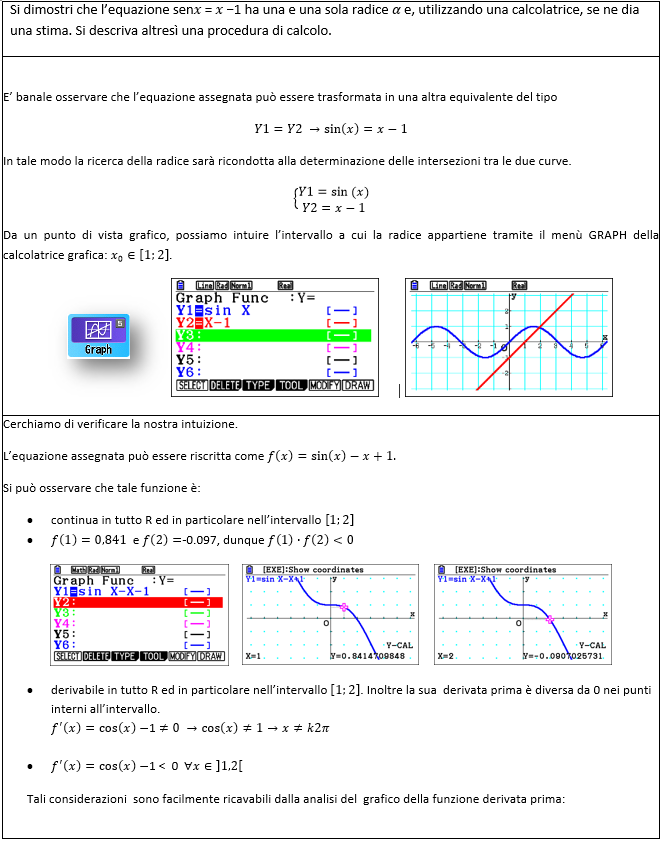
Costruendo, allora, le due curve si rendono visibili le radici cercate come ascisse dei punti di intersezione di queste due curve, come illustrano i due esempi che seguono

2) Determinazione della soluzione con metodi iterativi

Ricordiamo che affinché i metodi possano essere applicabili devono verificarsi le seguenti condizioni:

- la funzione deve ammettere uno zero nell’intervallo [a,b]
- la funzione deve essere continua nell’intervallo [a,b]
- f(a)∙f(b)

Per la risoluzione approssimata di equazioni utilizzeremo la calcolatrice grafica Casio FX CG50.

Utilizzeremo la macchina calcolatrice sia per la visualizzazione delle radici cercate, sia per impostare le relazioni ricorsive evitando in tal modo calcoli tediosi (in accordo con le linee guida del 2010, “Ferma restando l’importanza dell’acquisizione delle tecniche, è necessario evitare dispersioni in tecnicismi ripetitivi o casistiche sterili che non contribuiscono in modo significativo alla comprensione dei problemi” – D.P.R. 15 marzo 2010, n. 89).