Matematica Maturità: equazione retta tangente a grafico di funzione

Prepararsi con anticipo alla prova di matematica della maturità è fondamentale. Dunque, perchè non esercitarsi con calcolo dell'equazione della retta tangente al grafico di una funzione? Questo, infatti, è uno dei quesiti di matematica più frequenti all'esame di maturità del liceo scientifico.

Il prof di matematica, Francesco Bologna, ci spiega come affrontare questo problema sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.

Scopri tutte le tracce della maturità scientifica degli anni passati

Impara ad usare la calcolatrice, guarda il nostro video!

Per determinare tale equazione dobbiamo ricordare il significato geometrico di derivata secondo il quale la derivata prima di una funzione in un punto rappresenta l'inclinazione della retta tangente in quel punto.

La procedura di calcolo si basa, in genere, su diverse fasi:

1. Si determina il valore della funzione in
[math]x_0,[/math]
[math]y_0=f\left(x_0\right);[/math]

2. Si determina l'equazione della funzione derivata prima
[math]y=f^{'}\left(x\right);[/math]

3. Si determina il valore della funzione derivata prima in
[math] x_0,[/math]
[math] y_0=f'\left(x_0\right),[/math]
in tal modo determiniamo il coefficiente angolare
della retta
[math]m.[/math]

4. Si determina l'equazione della tangente al grafico nel punto
[math]\left(x_0,y_0\right)[/math]
sostituendo i valori precedentemente determinati nella relazione del fascio proprio:

CALCOLO DELL'EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO DI UNA FUNZIONE

Esempio: determinare l'equazione della retta tangente al grafico della funzione

Nel punto di ascissa 10.

Determiniamo il valore della funzione in

sostituendo 10 al posto
di Otterremo:

Determiniamo l'equazione della funzione derivata prima

(ricorda che è una funzione composta)

Calcoliamo il valore del coefficiente angolare sostituendo 10 al posto della

Otterremo l'equazione della retta tangente al grafico nel punto

sostituendo i valori precedentemente determinati nella relazione del fascio proprio:

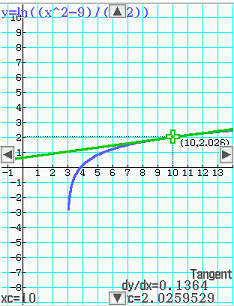
Vediamo come la calcolatrice FX991ES PLUS può semplificare la procedura.

Passaggio #1

Data la funzione, terminiamo determiniamo il valore della funzione in 10, sostituendo 10 al posto di

Dopo aver trascritto la funzione utilizzando la funzione ALPHA

Digita il comando CALC

E inserisci il valore 10 e digita =. Otterremo il valore dell'ordinata.

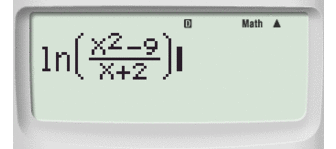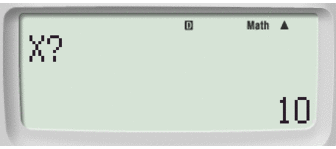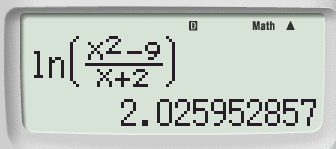
Passaggio #2

Utilizziamo la funzione SHIFT per inserire il comando di calcolo della derivata prima nel punto.

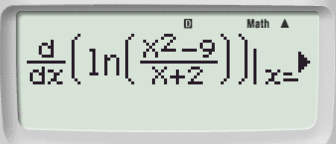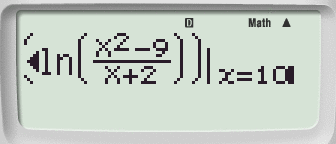
Passaggio #3

Digitando =

determineremo il valore della derivata nel punto, quindi il coefficiente angolare

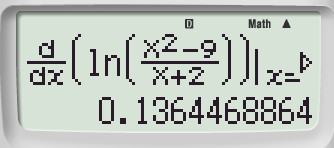
Passaggio #4

Sostituendo i valori precedentemente determinati nella relazione del fascio proprio

Otterremo l'equazione cercata.