Maturità 2018, impara a usare la calcolatrice grafica per risolvere le tracce della seconda prova di matematica

In questi ultimi anni le tipologie di prove dell'esame di Maturità sono leggermente cambiate rispetto al passato. Al liceo scientifico, ad esempio, allo scritto di Matematica si è passati da problemi e quesiti incentrati molto sulla teoria a tracce che partono da una dimensione più pratica. Spesso, infatti, gli studenti devono trovare soluzioni partendo da una situazione tratta dalla realtà e devono dimostrare di saper applicare le nozioni imparate in classe a casi e problemi concreti. Il cambiamento, quindi, non è da poco, e proprio per questo motivo gli anni scorsi il Ministero ha proposto delle simulazioni della seconda prova di matematica per le scuole. Di seguito proponiamo la risoluzione della simulazione del 2016 con il supporto della calcolatrice grafica CASIO FX-CG50.

PROBLEMA 1 con risoluzione
Le centraline di controllo del Po a Pontelagoscuro (FE) registrano il valore della portata dell'acqua, ovvero il volume d'acqua che attraversa una sezione trasversale del fiume nell'unità di tempo. Come responsabile della sicurezza della navigazione fluviale in quel tratto del Po, devi valutare quando consentire la navigazione stessa, in considerazione delle condizioni atmosferiche e del livello dell’acqua. Nel corso dell'anno le portate medie del Po (a Pontelagoscuro) sono di circa 34 milioni di m 3 al giorno in regime di magra, 130 milioni di m 3 al giorno in regime normale con un’oscillazione del 10% e 840 milioni di m 3 al giorno in regime di piena (fonte deltadelpo.net).
Durante un periodo di alcuni giorni di piogge intense, dalle rilevazioni registrate risulta che:
• nei primi due giorni dall'inizio delle misurazioni il valore della portata dell'acqua si è alzato dal valore di regime normale di 130 milioni di m 3 al giorno fino al valore massimo di 950 milioni di m 3 al giorno;
• nei giorni successivi la portata si è ridotta, tornando verso il valore di regime normale, inizialmente più velocemente e poi più lentamente.
1. Indicando con t il tempo, misurato in giorni, fissa un adeguato sistema di riferimento cartesiano in cui rappresentare il grafico dell'andamento della portata. Verifica se una delle seguenti funzioni può essere usata come modello per descrivere tale andamento, tenendo conto dei valori rilevati e del punto di massimo, giustificando con opportune argomentazioni sia la scelta che l'esclusione.

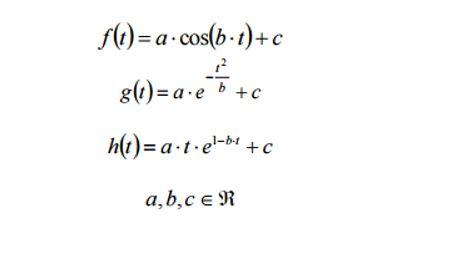
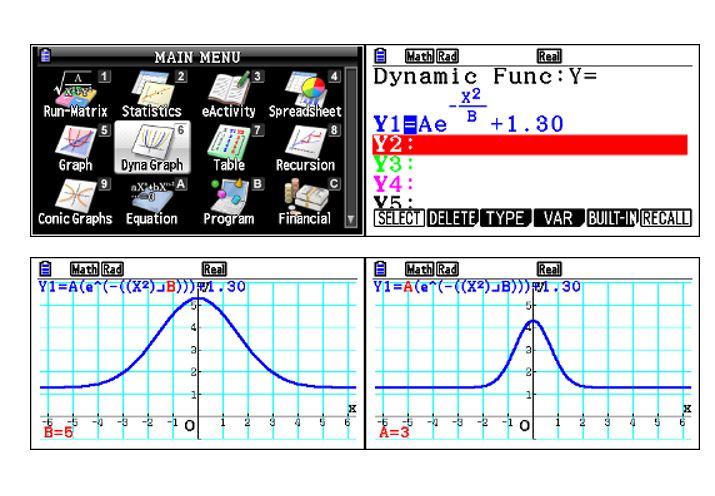
La scelta della funzione che meglio può essere utilizzata come modello per descrivere l’andamento, può essere supportata da una analisi grafica dinamica attraverso il menù Dyna Graph.

Dai dati forniti si evince che, per t che tende a più infinito, la funzione deve tendere al valore di regime pari a y=130, dunque deve essere presente un asintoto orizzontale.
Come si può dedurre visivamente, data la natura sinusoidale della funzione, non sono presenti asintoti orizzontali dunque la funzione non è adatta a descrivere il modello.
Procediamo con l’analizzare la seconda funzione.
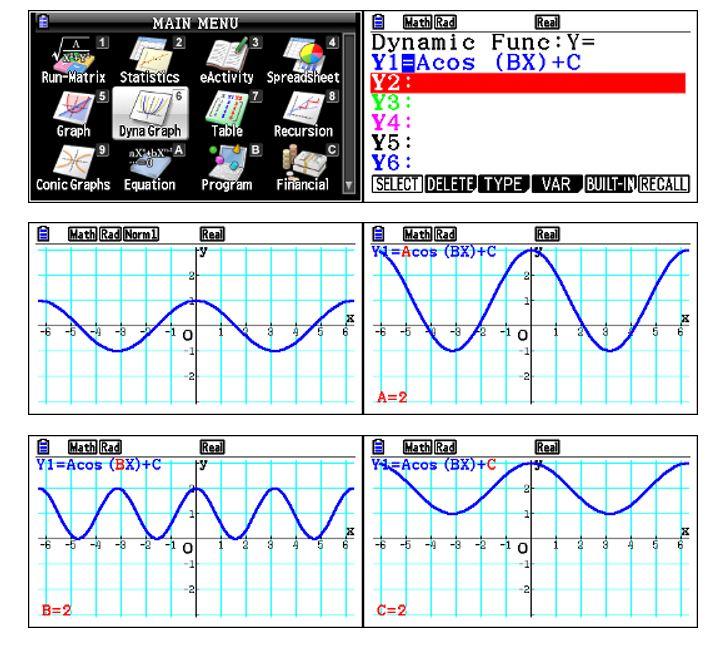
Inseriamo la seconda funzione utilizzando sempre il menù Dyna Graph.
Dalle informazioni date la funzione deve avere un valore iniziale coincidente con quello di regime pari a 130.
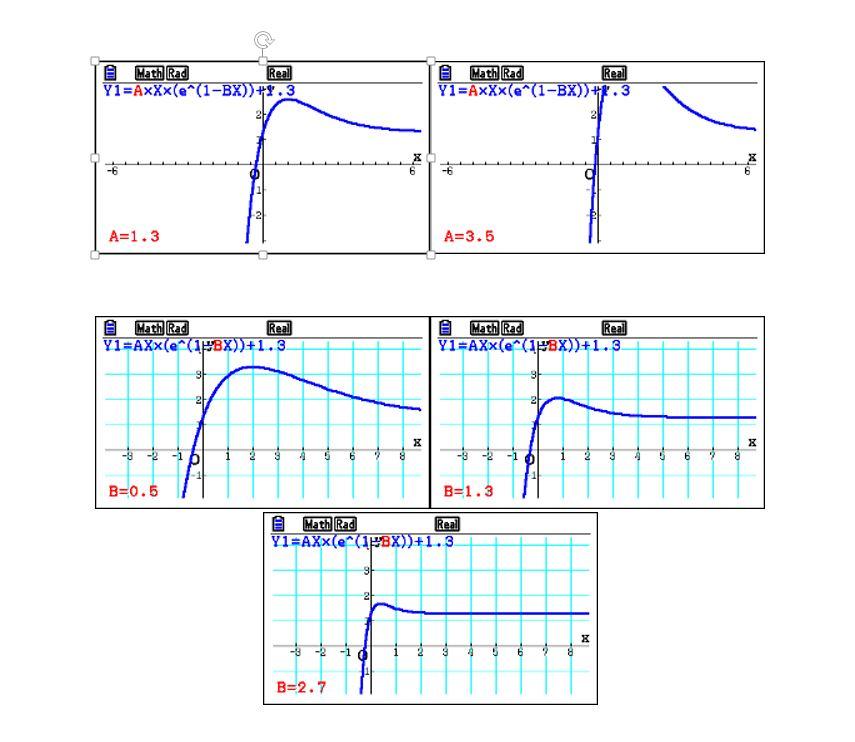
Analizzando il grafico della funzione, in particolare prestando attenzione all’impatto dei parametri A e B, si evince chiaramente che all’istante iniziale si otterrà sempre un valore maggiore di 130 a meno che non si ammetta un valore nullo per A.

Analizziamo la terza funzione.
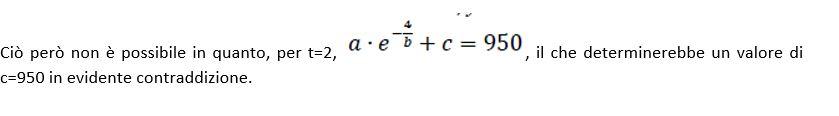
Inizialmente possiamo utilizzare il menù TABLE (ponendo A e B uguale a 1).

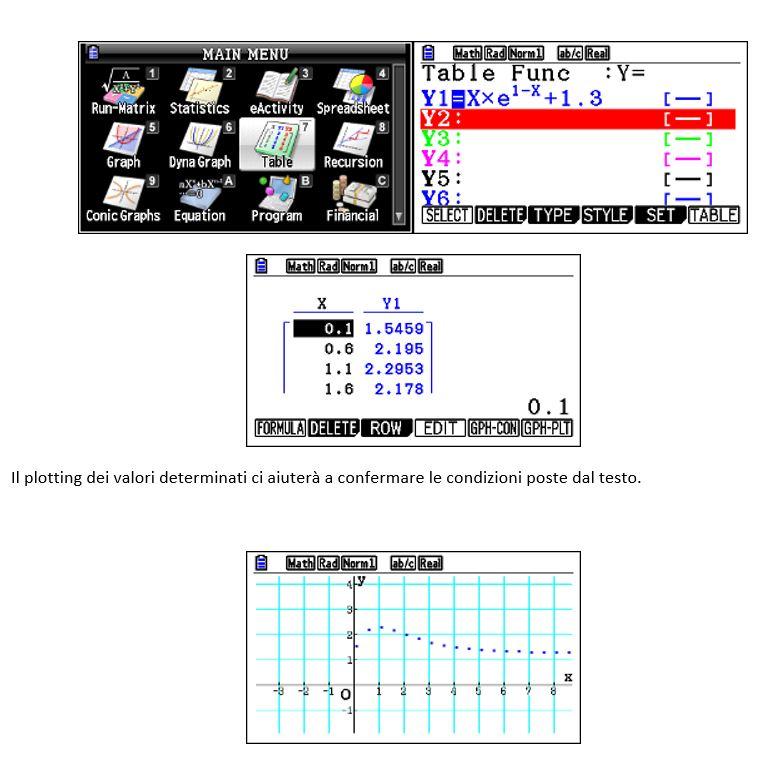
Utilizzando nuovamente il menù Dyna Graph, potremo valutare l’impatto dei parametri A e B sull’andamento grafico.

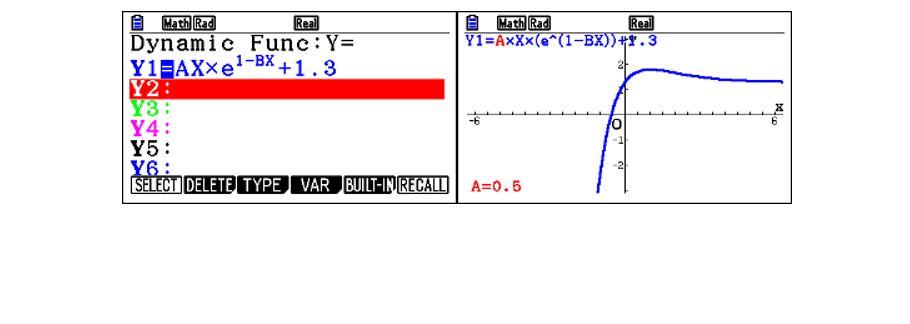
2. Individuata la funzione, determina i parametri in modo che siano verificate le condizioni sopra descritte per la portata e tracciane il grafico.

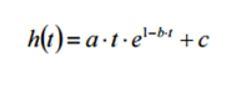
A=0 risulta evidente che C=130.
Calcoliamo la derivata prima e imponiamo che per t=2 ci sia un massimo.

3. Studia la variazione della portata nel tempo e valuta dopo quanti giorni tale variazione raggiunge il suo minimo. Inoltre, dovendo prevedere quando autorizzare la ripresa della navigazione in condizioni di sicurezza, valuta, analiticamente o per via grafica, dopo quanti giorni la portata rientra nel limite di oscillazione del valore di regime normale.

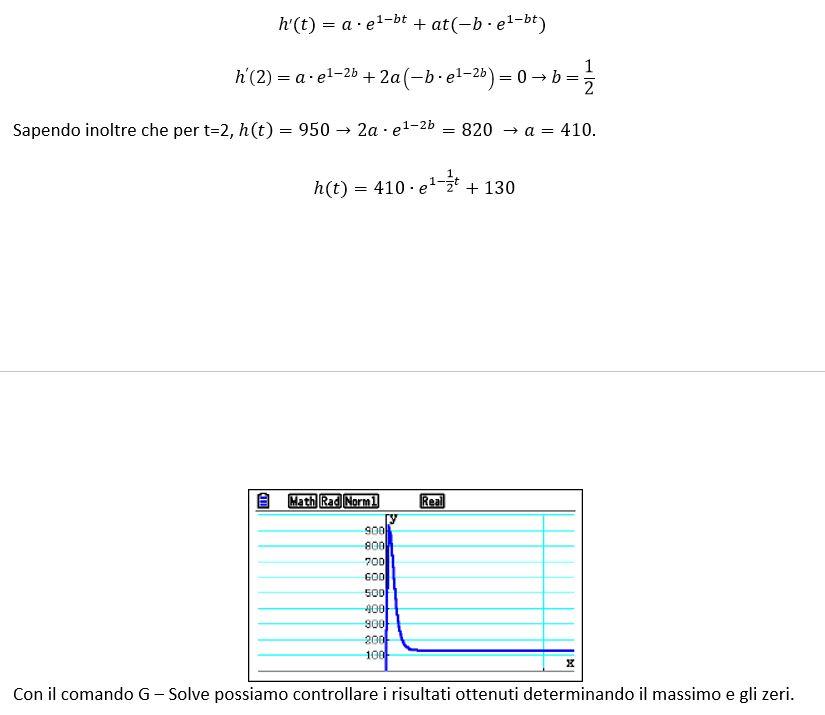
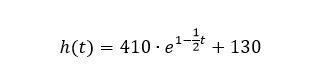
La variazione della portata nel tempo altro non è che la derivata della funzione.
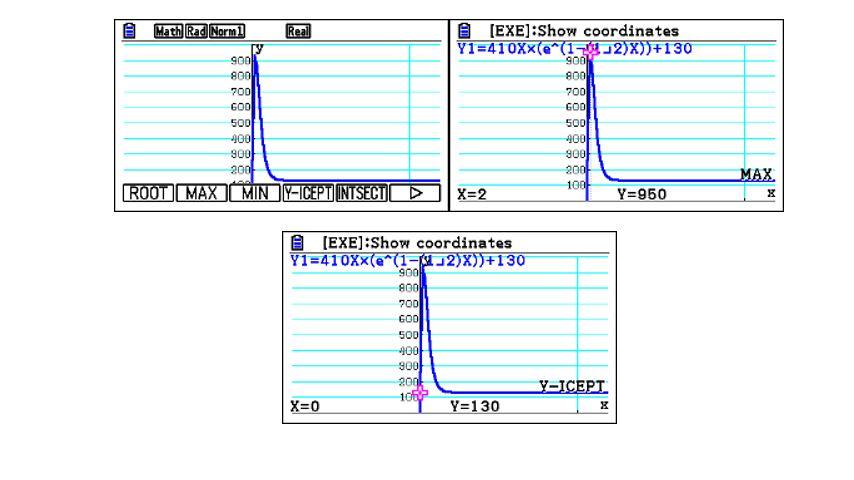
Attraverso il menù GRAPH determiniamone l’andamento grafico e analizziamo il tutto con il comando G- Solve.

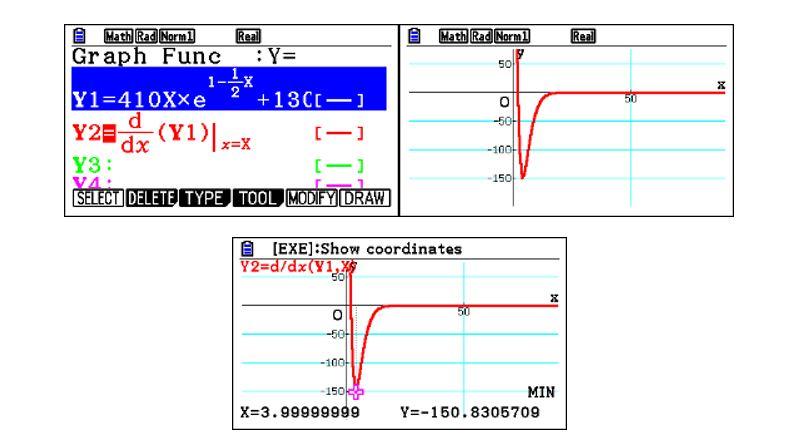
La funzione presenta un minimo per x=4, dunque dopo 4 giorni la variazione della portata nel tempo raggiunge il suo minimo.
Il valore di regime normale corrisponde a 130 +/- 10%, dunque tra 117 e 143.
Dovendo prevedere quando autorizzare la ripresa della navigazione in condizioni di sicurezza, valutiamo graficamente dopo quanti giorni la portata rientra nel limite di oscillazione del valore di regime normale, utilizzando il menù GRAPH.

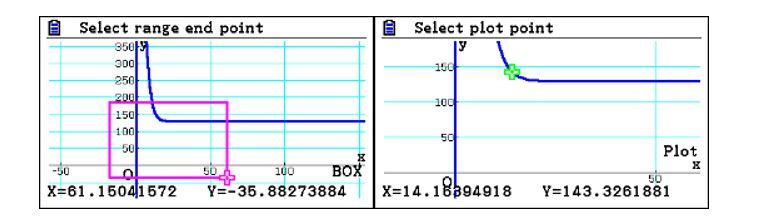
4. Nel tempo trascorso tra l’inizio del fenomeno e il rientro nei limiti normali, qual è il volume di acqua che ha superato il valore di regime normale?
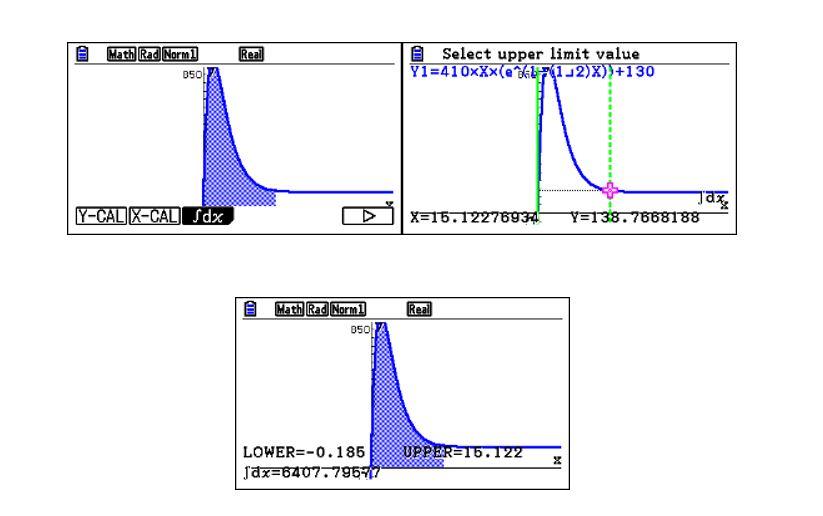
Il volume possiamo stabilirlo come area sottesa alla curva di h(t).

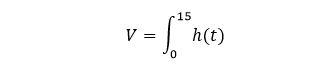
Utilizzando il comando G- Solve del menù GRapf, si otterrà un valore di circa 6400 milioni di metri cubi.

Considerando come valore di regime normale 143 ( in 15 giorni 143∙15=2145), il volume di acqua che ha superato il valore di regime normale è pari a 6387−2145=4242 milioni di metri cubi.