In quest'appunto di geometria troverai informazioni generali sul calcolo del perimetro e un'applicazione relativa a un rettangolo avente la base il doppio dell'altezza.
Indice
Cosa sono le figure piane e quali sono
In geometria tutto ruota intorno a tre enti, chiamati enti fondamentali.
Essi sono:
- il punto, il quale non presenta una dimensione ma serve esclusivamente per indicare una posizione
- la retta, avente solo la lunghezza. Essa è formata da infiniti punti disposti lungo la stessa direzione
- il piano, definito da larghezza e lunghezza.
Il piano è il tipo di ente di cui è possibile definire il perimetro e l'area. Le figure geometriche che presentano soltanto due dimensioni prendono il nome di figure piane. In geometria, esistono anche i solidi, ossia figure geometriche che presentano anche la terza dimensione(profondità).
Ritornando alle figure piane, esse sono:
- il triangolo, che presenta tre lati e tre angoli. Se i lati sono tutti uguali prende il nome di triangolo equilatero, se invece ha soltanto due lati uguali si chiama isoscele. Se tutti i lati sono diversi, si parla di triangolo scaleno. Per quanto riguarda gli angoli, se un triangolo presenta un angolo di [math]90°[/math], prende il nome di triangolo rettangolo
- il quadrato, che presenta quattro lati e quattro angoli uguali
- il rettangolo, con quattro angoli uguali e i lati opposti uguali
- il rombo
- il cerchio, l'unica figura piana ad essere racchiusa in una curva e non in una spezzata
- il parallelogramma, il quale ha i lati paralleli uguali
Oltre a questi, sono presenti anche altre figure piane più complicate, come il trapezio, il pentagono, l'esagono etc. Questi ultimi risultano regolari se presentano tutti gli angoli e tutti i lati congruenti.
Il calcolo del perimetro e dell'area di una figura piana
Come abbiamo già anticipato, poiché una figura piana presenta due dimensioni, è possibile calcolarne l'area e il perimetro. In particolare:
- il perimetro misura la lunghezza del contorno della figura piana. Per questo motivo è espresso utilizzando il metro ([math]m[/math]) o i suoi sottomultipli
- l'area misura l'estensione della superficie racchiusa all'interno del perimetro. L'unità di misura utilizzata per questa grandezza è il metro quadrato ([math]m^2[/math])
Ecco le formule per il calcolo dell'area e del perimetro delle principali figure piane.
Le formule sul triangolo
In generale, il perimetro del triangolo si calcola come la somma della lunghezza dei tre lati, ossia
, dove
è il perimetro e
sono i lati del triangolo.
L'area, invece, si calcola facendo il prodotto della base e dell'altezza diviso due, ossia
, dove
è la base del triangolo,
è l'altezza relativa alla base.
Le formule sul quadrato
Il quadrato presenta tutti i lati e gli angoli uguali. Per questo motivo il perimetro si calcola semplicemente moltiplicando per 4 la lunghezza di un lato, ossia
, mentre la superficie si quantifica moltiplicando la lunghezza del lato per se stesso, cioè
.
Le formule sul rettangolo
Il rettangolo presenta i lati opposti di lunghezza uguale e tutti gli angoli congruenti. Quindi il perimetro può essere calcolato come la somma del doppio della base e del doppio dell'altezza, cioè
, dove
è la base e
è l'altezza del rettangolo.
Dopo aver descritto la teoria, passiamo alla presentazione di un semplice esercizio per fissare i concetti.
Esempio: calcola il perimetro del rettangolo
Calcola il perimetro di un rettangolo che ha la base il doppio dell'altezza e la differenza fra le due misure è 15,5cm.
Svolgimento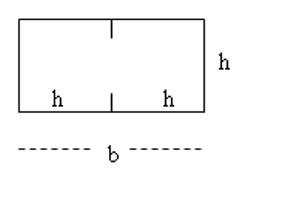 
Poiché la base è due volte l'altezza, la differenza è un segmento pari all'altezza, quindi h è proprio la differenza 15,5cm.
La base è il doppio, quindi 31cm.
Definite base e altezza, bisogna calcolare il perimetro. Esso sarà, quindi:
Per ulteriori approfondimenti sul perimetro del rettangolo vedi anche qua
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
