Come si definisce il seno di un angolo

In quest'appunto potrai trovare una descrizione della funzione seno, con esempi relativi agli angoli fondamentali

Come definire geometricamente il seno e il coseno di un angolo

Considero la circonferenza goniometrica

: essa è una circonferenza che ha il centro nell'origine degli assi e raggio unitario. Se prendo un punto sulla circonferenza di coordinate , esso si definirà come "estremo libero dell'arco".

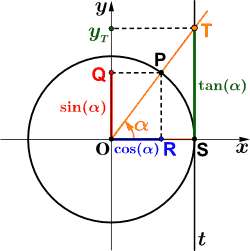
Se proietto il punto

sull'asse delle ascisse ottengo il segmento ; mentre se lo proietto sull'asse delle ordinate ottengo il segmento .

Il valore del seno dell'angolo

rappresenta il rapporto tra la distanza e la base del triangolo, mentre il valore del coseno corrisponde al rapporto tra la distanza dall'asse delle ordinate e la base del triangolo.

In termini matematici:

. Il seno si definisce come l'ordinata dell'estremo libero dell'arco .
Per quanto riguarda il coseno, invece, possiamo scrivere che .

Il valore del coseno corrisponde all'ascissa dell'estremo libero dell'arco

, mentre il seno corrisponde all'ordinata.

Valori di seno e coseno degli angoli fondamentali

In matematica, esistono delle equazioni chiamate equazioni trigonometriche. Per risolvere correttamente, è necessario conoscere il valore delle funzioni seno e coseno corrispondenti agli angoli fondamentali, cioè a .
In particolare, essi sono:

• [math]sen(0) = 0[/math]
• [math]sen(\frac{\pi}{2}) = 1[/math]
• [math]sen(\pi) = 0[/math]
• [math]sen(\frac{3\pi}{2}) = -1[/math]

Il seno assume sempre gli stessi valori, una volta compiuto un giro completo della circonferenza goniometrica. Infatti la funzione seno si definisce come una funzione periodica, di periodo

.

I valori del coseno degli angoli fondamentali sono invece:

• [math]cos(0)=1[/math]
• [math]cos(\frac{\pi}{2})=0[/math]
• [math]cos(\pi)=-1[/math]
• [math]cos(\frac{3\pi}{2})=0[/math]

Anche il coseno assume sempre gli stessi valori, essendo una funzione periodica di periodo

. Tuttavia, quando il seno è massimo il coseno è minimo e viceversa. Le funzioni seno e coseno non sono in fase: la prima anticipa la seconda di .

Il segno e l'andamento della funzione seno e coseno

La funzione seno rappresenta l'ordinata del punto trovato. Per questo motivo, guardando il sistema di riferimento cartesiano considerato, è possibile dire che il seno assume seno positivo nel primo e nel secondo quadrante e segno negativo nel terzo e nel quarto quadrante.

La funzione che rappresenta la funzione seno prende il nome di sinusoide:

Essa ha le seguenti caratteristiche:

• passa per i punti
  [math]O(0;0); A(\frac{\pi}{2};1); B(\pi;0); C(\frac{3\pi}{2}; 0); D(2\pi;0)[/math]
• crescente da
  [math]0[/math]
  a
  [math]\frac{\pi}{2}[/math]
  , decrescente da
  [math]\frac{\pi}{2}[/math]
  a
  [math]\frac{3\pi}{2}[/math]
  e nuovamente crescente da
  [math]\frac{3\pi}{2}[/math]
  a
  [math]2\pi[/math]

Al contrario, la funzione coseno è costituita dall'ascissa del punto trovato. Osservando il sistema di riferimento, in questo caso possiamo affermare che il segno del coseno èpositivo nel primo e nel quarto quadrante ed ènegativo nel secondo e nel terzo quadrante.

Per quanto riguarda l'andamento, invece, la funzione coseno ha le seguenti caratteristiche:

• interseca gli assi nei punti
  [math]A(0;1),B(\frac{\pi}{2};0),C(\frac{3\pi}{2};0),D(\frac{5\pi}{2};0))[/math]
• l'andamento della funzione è decrescente da
  [math]0[/math]
  a
  [math]\pi[/math]
  , risulta crescente tra
  [math]\pi[/math]
  e
  [math]2 \pi[/math]
  e di nuovo decrescente tra
  [math]2 \pi[/math]
  e
  [math]3\pi[/math]

Per ulteriori approfondimenti sulle funzioni seno e coseno vedi anche qua