Quadrilateri: definizione, classificazione e principali teoremi

In questo appunto troverai un riassunto delle proprietà e dei teoremi relativi ai quadrilateri, suddivisi per figura di riferimento.

Cos'è il parallelogrammo e quali sono le principali proprietà

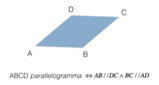
Secondo la definizione rigorosa, si definisce parallelogramma un quadrilatero avente i lati opposti paralleli.
Le condizioni necessarie affinché un quadrilatero si possa definire un parallelogramma sono:

• ogni diagonale del quadrilatero lo divide in due triangoli congruenti
• i lati opposti del quadrilatero sono congruenti
• gli angoli opposti sono congruenti
• gli angoli adiacenti sono supplementari, ossia la somma delle loro ampiezze corrisponde a 180°
• le diagonali si incontrano nel loro punto medio

Per stabilire se un quadrilatero è un parallelogramma, possono essere utilizzati diversi modi.

Uno tra questi è fornire una condizione sufficiente.
In particolare, se un quadrilatero convesso ha:

• i lati opposti congruenti, oppure
• gli angoli opposti congruenti, oppure
• le diagonali che si incontrano nel loro punto medio, oppure
• due lati opposti congruenti e paralleli

allora è un parallelogramma

Cos'è un rettangolo e quali sono le principali proprietà

Un rettangolo è, secondo la definizione, un parallelogramma avente i quattro angoli congruenti.
Le sue diagonali presentano una proprietà, ossia sono congruenti.
Per questo motivo, è condizione sufficiente affinché un parallelogramma sia un rettangolo che abbia le diagonali congruenti.

Teorema sui rettangoli

In un triangolo rettangolo la mediana relativa all'ipotenusa è congruente a metà ipotenusa.

Per quanto riguarda le altezze del rettangolo, invece, esse non sono altro che distanze tra rette parallele, poiché sono segmenti perpendicolari (gli angoli del rettangolo sono tutti retti e congruenti) a due lati opposti. Le due altezze sono uguali poiché date due rette parallele, ogni punto di ciascuna retta ha la stessa distanza dall'altra.

Cos'è il rombo e quali sono le sue proprietà

Si definisce un rombo un parallelogramma avente i quattro lati congruenti. Anche nel caso del rombo le diagonali hanno delle proprietà particolari, ossia sono perpendicolari fra loro e bisettrici degli angoli.

Per comprendere se un parallelogramma sia un rombo è possibile sfruttare le condizioni sufficienti. In particolare esse sono:

• se un parallelogramma ha le diagonali perpendicolari, allora è un rombo
• se un parallelogramma ha una diagonale bisettrice di un angolo, allora è un rombo

Cos'è un quadrato e quali sono le proprietà

Per definizione, un quadrato è un parallelogramma avente i quattro lati e i quattro angoli congruenti. Anche le diagonali del quadrato godono di una proprietà, ossia sono congruenti, sono perfettamente perpendicolari tra loro e bisettrici degli angoli.

Per comprendere se un quadrilatero possa essere un quadrato, bisogna individuare una condizione sufficiente.
In particolare, se un parallelogramma ha:

• le diagonali risultano congruenti e perpendicolari
• Le diagonali sono congruenti e una di esse è bisettrice di un angolo

allora è un quadrato.

Cos'è un trapezio e come riconoscerlo

Si definisce trapezio un quadrilatero aventi due soli lati paralleli. Esistono diversi tipi di trapezio, ossia:

• il trapezio isoscele, ossia un trapezio avente i lati obliqui congruenti. A questa tipologia è collegato un teorema, secondo cui in un trapezio isoscele gli angoli adiacenti a ciascuna base risultano congruenti. Vale anche il contrario, ossia se in un trapezio gli angoli adiacenti a una delle due basi sono congruenti, allora il trapezio è isoscele.
• il trapezio rettangolo, il quale presenta uno dei due lati perpendicolare alle basi

Casi particolari di segmenti congruenti nei triangoli e nei trapezi

Si definisce fascio improprio di rette l'insieme di tutte le rette parallele a una retta data. Esiste un teorema correlato a questo concetto, ossia: dato un fascio di rette tagliato da due trasversali, a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull'altra trasversale.

Sfruttando questo teorema è possibile ricavare alcuni casi particolari di segmenti congruenti all'interno del triangolo e del trapezio.

Il segmento con estremi nei punti medi dei lati di un triangolo

Se in un triangolo si congiungono i punti medi di due lati, il segmento che si ottiene è parallelo al terzo lato e congruente alla sua metà.

Il segmento con estremi nei punti medi dei lati di un trapezio

In un trapezio, il segmento congiungente i punti medi dei lati obliqui è parallelo alle due basi e congruente alla loro semisomma.

Esercizio di ricapitolazione sui quadrilateri

Non tutte le seguenti affermazioni sono vere: scopri quale o quali risultano false

• Basta una sola condizione sufficiente vera per rendere valida un'uguaglianza
• In un trapezio isoscele le basi sono uguali e i lati obliqui sono differenti
• In un triangolo rettangolo la mediana relativa all'ipotenusa è pari a metà ipotenusa.
• se un parallelogramma ha le diagonali parallele, allora è un rombo
• Se un parallelogramma ha le diagonali congruenti e una di esse è bisettrice di un angolo, allora è un rettangolo.

Soluzione dell'esercizio

La seconda e l'ultima affermazione sono sbagliate, poiché:

• In un trapezio isoscele le basi sono differenti mentre i lati obliqui devono avere la stessa lunghezza
• Un parallelogramma avente le diagonali congruenti e una di esse è bisettrice di un angolo si definisce rettangolo

Per ulteriori approfondimenti sui quadrilateri vedi anche qua