Le curve nel piano sono descritte spesso come punti che si muovono seguendo certe condizioni. Per esempio, la ipocicloide è generata da un punto sulla circonferenza di un cerchio che rotola internamente alla circonferenza di un cerchio più grande.
Incominciamo disegnando un piccolo cerchio di raggio all'interno di uno più grande di raggio
.
Raggi dei cerchi:
Useremo
per disegnare il cerchio più grande ed
per quello più piccolo.
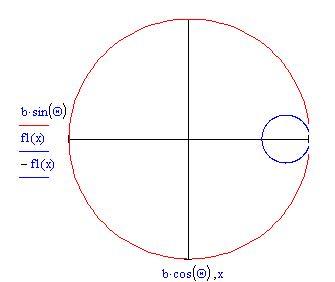
dove
è l'angolo formato dalla linea che congiunge l'origine ed il centro del cerchio interno e l'asse
. La curva sarà
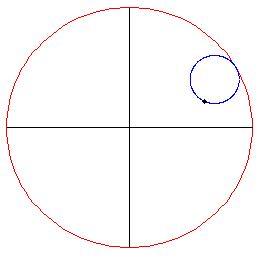
. Abbiamo bisogno di poter disegnare il cerchio rotante in qualsiasi posizione
.
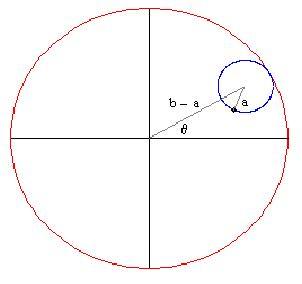
In tale posizione il nostro cerchio ha centro
Usando l'equazione del cerchio
Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in ogni posizione
Cambiando
qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono espressi in radianti.)
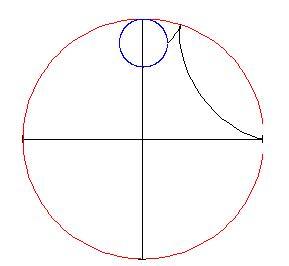
.
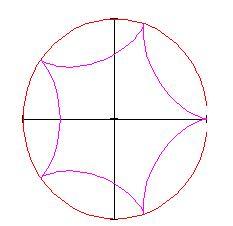
Ipocicloide :
generata da un punto del cerchio di raggio a che rotola all'interno del cerchio di raggio b
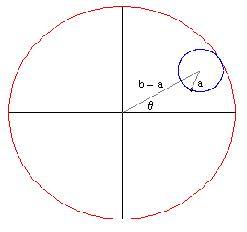
animazione a cura di Carlo Elce
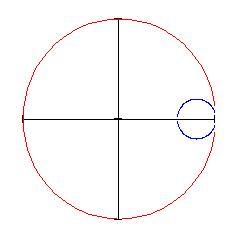
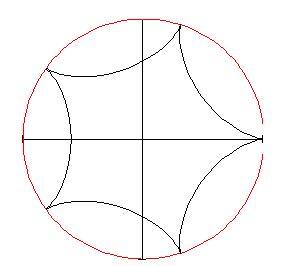
determina il numero di cuspidi presenti nel grafico. Se imposti
grande — diciamo 100 — vedrai un grafico di questo genere:
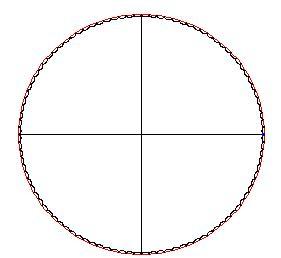
non è un intero, il punto sul cerchio rotante non tornerà al punto di partenza e se lo fai continuare a girare (poni
maggiore di 2 p ) vedrai un comportamento del genere:
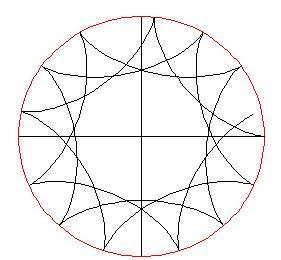
L'Ipocicloide
Le curve nel piano sono descritte spesso come punti che si muovono seguendo certe condizioni. Per esempio, la ipocicloide è generata da un punto sulla circonferenza di un cerchio che rotola inter...
Contenuto originale e autentico, validato dal Team di Esperti di Skuola.net










 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo