di _Steven

Ominide

2 min. di lettura

Vota 5 / 5

Si risolva

[math](\sqrtx+\sqrt{x-2}-1)/(\sqrt(x^2+3)-\sqrt(x+5)) ge 0[/math]

Questa disequazione va trattare studiando il comportamento di numeratore e denominatore separatamente.

Prendiamo il numeratore

[math]\sqrtx+\sqrt{x-2}-1 ge 0[/math]

Come dominio d'esistenza si ha

[math]x ge 2[/math]

e sostituendo

[math]x=2[/math]

si nota che è verificata, cioè

[math]\sqrtx+\sqrt{x-2} ge 1[/math]

Per

[math]x>2[/math]

è evidente che risulta verificata perchè i termini in

[math]x[/math]

possono solo aumentare. Quindi il numeratore è maggiore di zero per ogni valore del dominio

[math]x ge 2[/math]

Inoltre non potrà mai essere

[math]=0[/math]

perchè il dominio di esistenza lo esclude.

Ci siamo risparmiati la quadratura (bisognava effettuarne 2).

Pertanto, possiamo riassumere che il dominio coincide con l'insieme delle soluzioni, che è

[math]x>=2[/math]

Ora passiamo al denominatore

[math]\sqrt{x^2+3}-\sqrt(x+5)>0[/math]

Il dominio è

[math]x ge -5[/math]

Infatti il primo radicando risulta essere positivo per ogni

[math]x[/math]

Bisogna quindi verificare quando:

[math]\sqrt{x^2+3}>\sqrt(x+5)[/math]

Quadrando

[math]x^2+3>x+5[/math]

[math]x^2-x-2>0[/math]

Le radici dell'equazione associata sono

[math]x_(1,2)=(1+-\sqrt{1+8})/2=(1+-3)/2[/math]

[math]x_1=2[/math]

[math]x_2=-1[/math]

Dunque è verificata per

[math]x le -1[/math]

unito a

[math]x>2[/math]

(valori esterni).

In ogni caso dobbiamo eliminare l'intervallo

[math]x perchè dobbiamo tener conto del dominio del numeratore.

Perciò anche qui l'insieme delle soluzioni è

[math]x>2[/math]

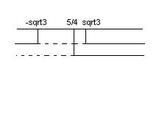
Ora osserviamo il quadro generale.

Il numeratore è sempre positivo, quindi la positività della frazione è assicurata solo se anche il denominatore è positivo.

In definitiva il risultato di

[math](\sqrtx+\sqrt{x-2}-1)/(\sqrt(x^2+3)-\sqrt(x+5)) ge 0[/math]

è:

[math]x>2[/math]

Escludiamo il caso

[math]x=2[/math]

perchè il denominatore si annulla per tale valore.

FINE

Disequazioni: (sqrtx+sqrt(x-2)-1)/(sqrt(x^2+3)-sqrt(x+5)) ge 0

Si risolva (sqrtx+sqrt(x-2)-1)/(sqrt(x^2+3)-sqrt(x+5)) ge 0 Questa disequazione va trattare studiando il comportamento di numeratore e denominatore separatamente. Prendiamo il numer...

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Appunti correlati

Disequazioni: sqrt(x^2+5)+sqrt(x^2-1)>0

Disequazioni: sqrt(x^2-3)-sqrt(4x-5) lt=0

Disequazioni: sqrt(x^2 - 1) < x + 3

Equazioni esponenziali e logaritmiche: Risolvere il seguente sistema di disequazioni esponenziali: left{ \begin{array}{rl} 7^x Â· \sqrt[x]{49} : \sqrt[3]{(frac{1}{7})^{-2x-5}} > 0 &\ \sqrt[3]{1 - 3 Â· 2^x Â· (2^x - 1)} - 2^x + 1 > 0 & end{array}\rig

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.