Determinare le soluzioni della seguente disequazione:
[math] \sqrt{x^2 - 1} > x + 3 [/math]
Svolgimento
Poiché il radicale è minore di un certo valore, dobbiamo impostare un sistema a tre disequazioni in questo modo:
[math][/math]
left{
egin{array}{ll}
x^2 - 1 ≥ 0& \
x + 3 > 0&\
(\sqrt{x^2 - 1})^2 end{array}
ight.
[math][/math]
left{
egin{array}{ll}
x^2 - 1 ≥ 0& \
x + 3 > 0&\
(\sqrt{x^2 - 1})^2 end{array}
ight.
[math][/math]
Cominciamo risolvendo la prima disequazione:
[math] x^2 - 1 ≥ 0 [/math]
Passiamo all'equazione associata e determiniamo le soluzioni:
[math] x^2 - 1 = 0 [/math]
[math] x^2 = 1 \to x = ± 1 [/math]
Prendiamo come soluzioni gli intervalli esterni alle radici, dato che la disequazione è maggiore o uguale a zero:
[math] S : x ≤ - 1 ∨ x ≥ 1 [/math]
La seconda disequazione è di risoluzione immediata:
[math] x + 3 > 0 \to x > - 3 [/math]
Passiamo ora alla terza:
[math] (\sqrt{x^2 - 1})^2 > (x + 3)^2 [/math]
[math] x^2 - 1 > x^2 + 9 + 6x [/math]
[math] x^2 - 1 - x^2 - 9 - 6x > 0 [/math]
[math] - 10 - 6x > 0 [/math]
[math] - 6x > 10 \to 6x > - 10[/math]
[math] x > - (10)/6 \to x > - 5/3 [/math]
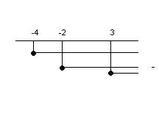
Torniamo al sistema e determiniamo le sue soluzioni:
[math][/math]
left{
egin{array}{ll}
x ≤ - 1 ∨ x ≥ 1&\
x > - 3&\
x > - 5/3 &
end{array}
ight.
[math][/math]
left{
egin{array}{ll}
x ≤ - 1 ∨ x ≥ 1&\
x > - 3&\
x > - 5/3 &
end{array}
ight.
[math][/math]
[math] S : - 5/3 > x ≤ - 1 ∨ x ≥ 1 [/math]
![Disequazioni: [math]\sqrt{{{x}^{2}+{2}}}-\sqrt{{{3}{x}-{1}}}>{4}{x}[/math]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/2017/10/dise_irra_e1.jpg)
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
