Anteprima
Vedrai una selezione di 1 pagina su 3
Regola di Ruffini - Scomposizione di un polinomio Pag. 1
1 su 3
Disdici quando vuoi 162x117
Disdici quando
vuoi
Acquista con carta
o PayPal
Scarica i documenti
tutte le volte che vuoi
Sintesi
In questo appunto viene spiegata la regola di Ruffini con attenzione agli aspetti principali legati alla regola medesima. Si spiega anche come deve essere scritta la regola e come la si deve applicare. la ricerca di una radice e gli aspetti principali.



Introduzione alla regola di Ruffini


La regola di Ruffini serve per scomporre un polinomio qualunque
[math] Pn(x)[/math]
di grado
[math] n>1[/math]
(solitamente maggiore di 3), o per dividere un polinomio
[math] P(x) [/math]
per un binomio del tipo
[math](x – a)[/math]
.
La particolarità della regola di Ruffini è che restituisce sempre i coefficienti di due polinomi,
[math] Q(x)[/math]
ed
[math]R(x)[/math]
, di grado rispettivamente
[math]1[/math]
ed
[math](n-1) [/math]
; dove n è il grado del polinomio
[math] P(x)[/math]
.




Quando utilizzare la Regola di Ruffini? Come applicarla?


In questa sezione vedremo come applicare, passo dopo passo, la regola di Ruffini.
La Regola di Ruffini, o Metodo di Ruffini, generalmente si applica ai polinomi di grado
[math] n>1 [/math]
. In realtà, bisogna considerare il fatto che, trattandosi di un metodo di calcolo più articolato di quelli che abbiamo visto per la classica scomposizione di un binomio, questo metodo si applica ogni qualvolta non è possibile attuare un metodo di scomposizione di un polinomio, oppure quando
[math] n>3 [/math]
. Vediamo adesso come fare!

Ricerca di una radice: per prima cosa cerchiamo una radice del polinomio
[math]P(x)[/math]
. Si chiama zero (o radice) di un polinomio
[math] P(x) [/math]
ogni valore
[math]r[/math]
che, attribuito alla variabile
[math]x [/math]
, rende nullo il polinomio. Dato un polinomio non nullo P(x) di grado n, della forma
[math] P(x) = a_n x^n+a _(n−1) x^(n−1)+...+a_1 x+ a_0 [/math]

con a_n coefficienti reali,
[math]P(x)[/math]
ammette al massimo n radici reali distinte. Le eventuali radici reali, se esistono, sono della forma
[math]r=\frac{p}{q}[/math]
.
Dove
[math]p[/math]
 è un divisore del termine noto
[math]a_0[/math]
; e
[math]q[/math]
 è un divisore del coefficiente
[math]a_n[/math]
.
Vediamo un esempio per capire meglio quanto detto!
Es:
[math] P(x)= x^3+3x^2+x-5 [/math]

In questo caso abbiamo un polinomio di grado
[math]n=3[/math]
, quindi al massimo possiamo trovare tre radici che, sostituite alla variabile
[math] x[/math]
, annullano il polinomio. Adesso dobbiamo trovare la nostra
[math]r[/math]
, e vediamo che
[math] a_n=1[/math]
e
[math]a_0=-5[/math]
. Quindi, dobbiamo prendere l'insieme di tutti quei numeri naturali che sono divisibili per
[math] a_n [/math]
e
[math] a_0 [/math]
, ovvero
[math]{1,-1,5,-5}[/math]
. Adesso sostituiamo ognuno di questi numeri alla variabile
[math]x [/math]
all'interno del polinomio e vediamo se lo annullano.


  • [math]P(1)=1+3+1-5=0 => 1 [/math]
    è radice del nostro polinomio;
  • [math]P(-1)=-1+3-1+5= 6 => -1 [/math]
    non è radice di
    [math]P(x)[/math]
    ;
  • [math]P(5)=125+3*25+5-5=200 => 5 [/math]
    non è radice di
    [math]P(x)[/math]
    ;
  • [math]P(-5)=-125+3*25-5-5= -60 => -5 [/math]
    non è radice di
    [math]P(x)[/math]
    .


per ulteriori approfondimenti sulla Regola di Ruffini vedi anche qua

In questo caso abbiamo trovato una radice del polinomio, ovvero
[math]r=1[/math]
, ma bisogna considerare il fatto che in alcuni casi il nostro polinomio potrebbe non ammettere radici razionali; come nel caso della somma di due quadrati.

Ad ogni modo, adesso che abbiamo trovato una radice, possiamo procedere con il metodo di Ruffini.

Applicazione del metodo: per applicare il metodo di Ruffini è necessario creare una tabellina in cui inseriamo nella prima riga (lasciando libera la prima colonna) i coefficienti a_n del polinomio
[math]P(x)[/math]
, in ordine decrescente da sinistra verso destra. Quindi scriveremo in ordine
[math] a_n, a_(n-1), a_(n-2),...., a_1, a_0 [/math]
. Nota bene: se nel polinomio di grado
[math]n=3[/math]
, manca il termine relativo al grado 1, allora avremo che
[math]a_1=0[/math]
.
Dopo di ché, scriviamo nella prima colonna della seconda riga la radice r del polinomio che abbiamo trovato precedentemente. Fatto ciò, ci spostiamo nella terza riga e, a partire dalla seconda colonna, iniziamo a completare la nostra tabella.
Per prima cosa riportiamo nella seconda colonna della terza riga il coefficiente del termine di grado massimo, ovvero a_n. Poi moltiplichiamo questo coefficiente per la radice
[math]r[/math]
, cioè
[math](a_n*r)[/math]
, e scriviamo il risultato sotto il coefficiente
[math]a_(n-1)[/math]
, cioè nella terza colonna della seconda riga. A questo punto facciamo la somma degli elementi della terza colonna, ovvero
[math]a_(n-1)+(a_n*r) [/math]
e riportiamo il risultato sotto, cioè nella terza colonna della terza riga. A questo punto ripetiamo quanto fatto precedentemente, fino ad arrivare all'ultima colonna, cioè al coefficiente del termine noto
[math]a_0 [/math]
.
L'ultimo elemento della tabella, cioè l'elemento che si trova nella n_esima colonna della terza riga, rappresenta il resto della scomposizione. Se non abbiamo commesso errori, allora il resto è nullo.
I valori che otteniamo nell'ultima riga non sono altro che i coefficienti del polinomio
[math]R(x) [/math]
di grado
[math](n-1)[/math]
. Mentre il polinomio di grado 1, sarà
[math]Q(x)=(x-r)[/math]
.

Esempio Svolto: Applicazione della regola di Ruffini


Nel paragrafo precedente abbiamo trovato la radice del polinomio
[math] P(x)= x^3+3x^2+x-5 [/math]
, ovvero
[math]r=1[/math]
. Adesso applichiamo la regola di Ruffini e costruiamo la nostra tabella per trovare
[math]Q(x)[/math]
ed
[math]R(x) [/math]
, tali che
[math]P(x)=Q(x)R(x)[/math]
.
Per prima cosa identifichiamo i coefficienti dei termini del polinomio e li scriviamo per grado decrescente, ovvero:
[math]
a_n=1
a_(n-1)=3
a_(n-2)=1
a_0=-5
[/math]




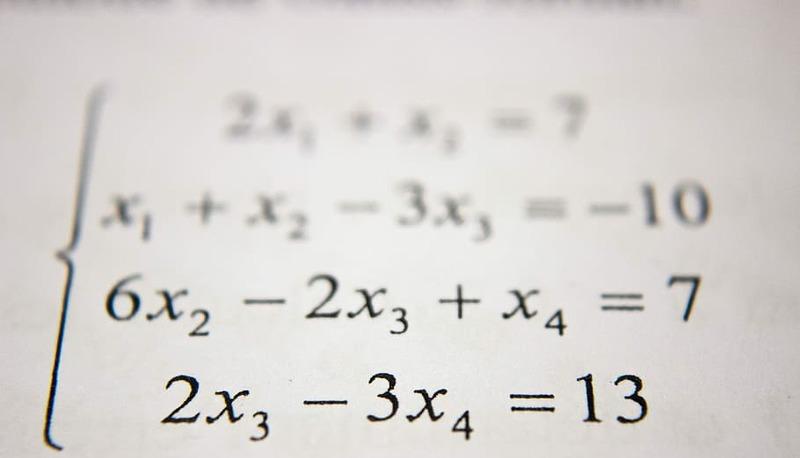
quindi nella prima riga della nostra tabella avremo:
[math]0 1 3 1 -5[/math]
(Ricorda che la prima colonna della prima riga deve rimanere vuota)
Per quanto detto prima, nella prima colonna della seconda riga scriviamo solo il resto, ovvero
[math]r=1[/math]
.
Passiamo adesso alla terza riga e scriviamo
[math]0 [/math]
nella prima colonna perché la prima colonna rimane vuota),
[math]1[/math]
nella seconda colonna perché riportiamo il coefficiente
[math]a_n [/math]
del polinomio.
Moltiplichiamo
[math]a_n*r= 1*1=1[/math]
e scriviamo
[math]1 [/math]
sotto il coefficiente
[math]a_(n-1)[/math]
, cioè nella terza colonna della seconda riga.
Sommiamo i coefficienti della terza colonna
[math]3+1=4[/math]
e riportiamo il risultato sotto, cioè scriviamo
[math]4 [/math]
nella terza riga della terza colonna.
Moltiplichiamo il numero appena ottenuto per il resto, quindi
[math]4*1=4[/math]
e riportiamo il risultato nella quarta colonna, cioè sotto il coefficiente
[math]a_(n-2)=1[/math]

Sommiamo i coefficienti della quarta colonna
[math]1+4=5 [/math]
e riportiamo il risultato sotto, cioè scriviamo
[math]5[/math]
nella terza riga della quarta colonna.
Moltiplichiamo il numero appena ottenuto per il resto, quindi
[math]5*1=5[/math]
e riportiamo il risultato nella quinta colonna, cioè sotto il coefficiente
[math] a_0=-5 [/math]

Sommiamo i coefficienti della quinta colonna
[math]-5+5=0 [/math]
e riportiamo il risultato sotto, cioè scriviamo
[math]0 [/math]
nella terza riga della quinta colonna.
Come potete vedere, il risultato dell'ultima operazione è zero, questo significa che il resto è nullo e quindi le operazioni effettuate sono corrette. Abbiamo ottenuto il nostro polinomio scomposto!
I valori ottenuti nell'ultima riga sono i coefficienti del polinomio
[math]R(x)[/math]
di grado
[math]2[/math]
. Quindi avremo che
[math]R(x)=x^2+4x+5 [/math]
, mentre
[math]Q(x)=x-1[/math]

Allora possiamo scrivere che
[math]P(x)=(x-1)(x^2+4x+5)[/math]
Estratto del documento

REGOLA DI RUFFINI

La regola di Ruffini serve per scomporre il polinomio A(x) o per dividere il polinomio A(x) per un binomio del tipo x

– a.

La particolarità della regola di Ruffini è che, in ambi i casi, restituisce i coefficienti di un polinomio Q(x) di grado n-1

rispetto al polinomio P(x).

Di seguito, sarà analizzata la scomposizione di un polinomio.

Sarà utilizzata la seguente convenzione: in nero si indicheranno le operazioni da fare, in corsivo (nero) si indicheranno

i richiami di algebra, utili a comprendere le operazioni da fare, mentre in rosso si indicheranno le operazioni effettuate.

Scomporre il polinomio A(x)

Scomporre un polinomio significa riscriverlo come prodotto di polinomio irriducibile.

Δ

Un polinomio è irriducibile se è di primo grado o di secondo grado con < 0

3 2

A(x) = x + 6x + 11x + 6 = B(x) C(x)

1) Ricercare le radici del polinomio tra i sottomultipli del termine noto.

Le radici del polinomio sono quei numeri che sostituiti alla variabile rendono il polinomio uguale a 0.

Se c è una radice di A(x) A(c) = 0

Il termine noto è il termine di grado 0, ovvero il numero scritto senza variabile.

Le radici sono da ricercarsi tra i sottomultipli del termine noto soltanto nel caso in cui il coefficiente del termine di

grado massimo è 1. Negli altri casi, le eventuali radici sono da ricercarsi tra i numeri razionali ± p/q dove p è un

sottomultiplo del termine noto e q è un sottomultiplo del coefficiente di grado massimo.

–

Una volta trovata la radice del polinomio c, si deduce che A(x) è divisibile per x c.

Un polinomio A(x) è divisibile per B(x) se il resto è uguale a 0.

Il resto di una divisione tra polinomi è il polinomio R(x) da dividere per B(x) e aggiungere a Q(x) per ottenere

A(x)/B(x). In simboli:

= Q(x) + ovvero A (x) = B(x )Q(x)+ R(x)

D(6) = ±1, ±2, ±3, ±6

P(-1) = -1 + 6 - 11 + 6 = 0

B(x) = x - (-1) = x + 1

3 2

A(x) = x + 6x + 11x + 6 = (x + 1) C(x)

2) Costruire una tabella formata da due barre verticali e una orizzontale, inserendo nella prima riga, della seconda

colonna, tutti i coefficienti del dividendo, ordinati secondo le potenze decrescenti, ad eccezione del termine noto,

Dettagli
Publisher
MiK194
3 pagine
91 download