Problemi con equazioni e sistemi di I e II grado: Il perimetro di un parallelogramma è 80a e la somma dei quadrati dei lati è 1700 a^2 ; determina le lunghezze dei lati del parallelogramma e quelle delle altezze ...

di _francesca.ricci

Ominide

3 min. di lettura

Vota

Il perimetro di un parallelogramma è

[math]80a[/math]

e la somma dei quadrati dei lati è

[math] 1700 a^2 [/math]

; determina le lunghezze dei lati del parallelogramma e quelle delle altezze sapendo che la differenza tra i quadrati delle altezze è

[math]256 a^2[/math]

Verifica che la diagonale minore è altezza del parallelogramma.

Svolgimento

Per prima cosa, chiamiamo con

[math]x[/math]

[math]y[/math]

i lati del parallelogramma:

[math] AB = CD = x [/math]

[math] BC = AD = y [/math]

Analizziamo i dati fornitici dal problema:

[math] AB + BC + CD + DA = 2 AB + 2 BC = 80 a [/math]

[math] AB^2 + BC^2 + CD^2 + DA^2 = 2 AB^2 + 2 BC^2 = 1700 a^2 [/math]

Possiamo già impostare un sistema con le prime due equazioni:

[math][/math]
left{ \begin{array}{rl}
2x + 2y = 80 a &\
2x^2 + 2y^2 = 1700 a^2 &
end{array}\right.
[math][/math]

Dividiamo tutto per due:

[math][/math]
left{ \begin{array}{rl}
x + y = 40 a &\
x^2 + y^2 = 850 a^2 &
end{array}\right.
[math][/math]

Ricaviamo un'incognita dalla prima equazione e risolviamo per sostituzione:

[math][/math]
left{ \begin{array}{rl}
x = 40 a - y &\
x^2 + y^2 = 850 a^2 &
end{array}\right.
[math][/math]

Sostituiamo nella seconda equazione:

[math] (40 a - y)^2 + y^2 = 850 a^2 [/math]

[math] 1600 a^2 + y^2 - 80 ay + y^2 = 850 a^2 [/math]

[math] 2y^2 - 80 ay + 750 a^2 = 0 [/math]

[math] y^2 - 40 ay + 375 a^2 = 0 [/math]

Troviamo le soluzioni con la formula ridotta

[math] y = frac(-b/2 Â± \sqrt{(b/2)^2 - ac})(a) [/math]

[math] k = frac(-(-40 a)/2 Â± \sqrt{((-40 a)/2)^2 - 375 a^2})(1) = 20 a Â± \sqrt(400a^2 - 375 a^2) = [/math]

[math] 20 a Â± \sqrt{25a^2} = 20a Â± 5a [/math]

[math] y_1 = 20a + 5a = 25a , y_2 = 20a - 5a = 15a [/math]

Troviamo ora i rispettivi valori di x:

[math] x_1 = 40a - 25a = 15a , x_2 = 40a - 15a = 25a [/math]

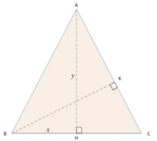
Sapendo che l'area del parallelogramma si trova moltiplicando la base per l'altezza; possiamo quindi scrivere:

[math] A_(ABCD) = AH \cdot AH = BC = AK [/math]

dove

[math]AK[/math]

è l'altezza relativa al lato

[math]BC[/math]

; inoltre sappiamo che:

[math] AK^2 - AH^2 = 256a^2 [/math]

Possiamo quindi impostare un sistema:

[math][/math]
left{ \begin{array}{rl}
25 a Â· AH = 15 a Â· AK &\
AK^2 - AH^2 = 256 a^2 &
end{array}\right.
[math][/math]

Ricaviamo dalla prima equazione uno dei due lati, e risolviamo il sistema per sostituzione;

[math][/math]
left{ \begin{array}{rl}
AH = frac{15 a Â· AK}{25 a} &\
AK^2 - AH^2 = 256 a^2 &
end{array}\right.
[math][/math]

Sostituiamo nella seconda equazione:

[math] AK^2 - (frac(15a \cdot AK)(25a) )^2 = 256 a^2 [/math]

[math] AK^2 - frac(225a^2 \cdot AK^2)(625a^2) = 256 a^2 [/math]

[math] 625a^2 \cdot AK^2 - 225a^2 \cdot AK^2 = 160000 a^4 [/math]

[math] 400 a^2 \cdot AK^2 = 160000 a^4 [/math]

[math] AK^2 = frac(160000 a^4)(400 a^2) = 400 a^2 \to AK = 20 a[/math]

Troviamo quindi il valore di

[math]AH[/math]

[math] AH = frac(15a \cdot 20a)(25a) = 12 a [/math]

Con il teorema di Pitagora possiamo verificare che la diagonale minore è altezza del parallelogramma:

[math] AC = \sqrt{AB^2 - CB^2} = \sqrt((25a)^2 - (15a)^2) = \sqrt(625a^2 - 225a^2) = [/math]

[math] \sqrt{400 a^2} = 20 a [/math]

Problemi con equazioni e sistemi di I e II grado: Il perimetro di un parallelogramma è 80a e la somma dei quadrati dei lati è 1700 a^2 ; determina le lunghezze dei lati del parallelogramma e quelle delle altezze ...

Problema di geometria con parametro risolvibile con sistemi di primo grado: determinare lati e altezze di una parallelogramma

Svolgimento

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Svolgimento

Appunti correlati

Problemi con equazioni e sistemi di I e II grado: Un triangolo isoscele ha un'area di 168 m^2 e l'altezza relativa a uno dei suoi lati obliqui è 1344cm . Determina la base del triangolo e l'altezza relativa alla base.

Problemi con equazioni e sistemi di I e II grado: In un triangolo isoscele la base supera di 2 cm l'altezza, mentre ciascuno dei due lati congruenti supera di 2 cm la base. Trova il perimetro e l'area del triangolo.

Problemi con equazioni e sistemi di I e II grado: Determina la lunghezza dei lati di un rettangolo di perimetro 280 cm inscritto in una circonferenza di raggio 50 cm .

Problemi con equazioni e sistemi di I e II grado: In un rettangolo la somma dell'altezza e di 1/3 della base è 15 cm; determina la lunghezza del perimetro, sapendo che l'area è di 168 cm^2 .

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.