In un rettangolo la somma dell'altezza e di
[math]1/3[/math]
della base è
[math]15 cm[/math]
; determina la lunghezza del perimetro, sapendo che l'area è di
[math]168 cm^2[/math]
.
Svolgimento
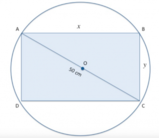
Chiamiamo i lati del triangolo con le incognite
[math]x[/math]
e
[math]y[/math]
:
[math]AD = BC = x[/math]
[math]AB = CD = y [/math]
Dalle informazioni forniteci dal problema possiamo dedurre che:
[math]AD + 1/3 AB = 15 cm [/math]
[math]AB \cdot BC = 168 cm^2 [/math]
Cioè:
[math] x + 1/3 y = 15 [/math]
[math] y \cdot x = 168 [/math]
Impostiamo un sistema:
[math][/math]
left{ \begin{array}{rl}
x +frac{1}{3} y = 15 &\
xy = 168 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
x +frac{1}{3} y = 15 &\
xy = 168 &
end{array}\right.
[math][/math]
Ricaviamo x dalla prima equazione e risolviamo per sostituzione:
[math][/math]
left{ \begin{array}{rl}
x = 15 - frac{1}{3} y &\
xy = 168 &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
x = 15 - frac{1}{3} y &\
xy = 168 &
end{array}\right.
[math][/math]
Lavoriamo sulla seconda equazione:
[math] (15 - 1/3 y) \cdot y = 168 [/math]
[math] 15y - 1/3 y^2 = 168 [/math]
[math] 45y - y^2 - 504 = 0 [/math]
[math] y^2 - 45y + 504 = 0 [/math]
Troviamo le soluzioni con la formula
[math] y = frac(-b ± \sqrt{b^2 - 4ac})(2a) [/math]
:
[math] y = frac(-(-45) ± \sqrt{(-45)^2 - 4 \cdot 504})(2) = frac(45 ± \sqrt(2025 - 2016))(2) = [/math]
[math] frac(45 ± \sqrt{9})(2) = frac(45 ± 3)(2) [/math]
[math] y_1 = frac(45 + 3)(2) = 24 , y_2 = frac(45 - 3)(2) = 21 [/math]
Troviamo i rispettivi valori di x:
[math] x_1 = 15 - 1/3 \cdot 24 = 7 , x_2 = 15 - 1/3 \cdot 21 = 8 [/math]
Determiniamo la lunghezza del perimetro nei due casi:
[math] P_1 = AB + BC + CD + DA = 2 AB + 2 BC = 2 \cdot 24 + 2 \cdot 7 = 62 cm [/math]
[math] P_2 = AB + BC + CD + DA = 2 AB + 2 BC = 2 \cdot 21 + 2 \cdot 8 = 58 cm [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
