vuoi
o PayPal
tutte le volte che vuoi
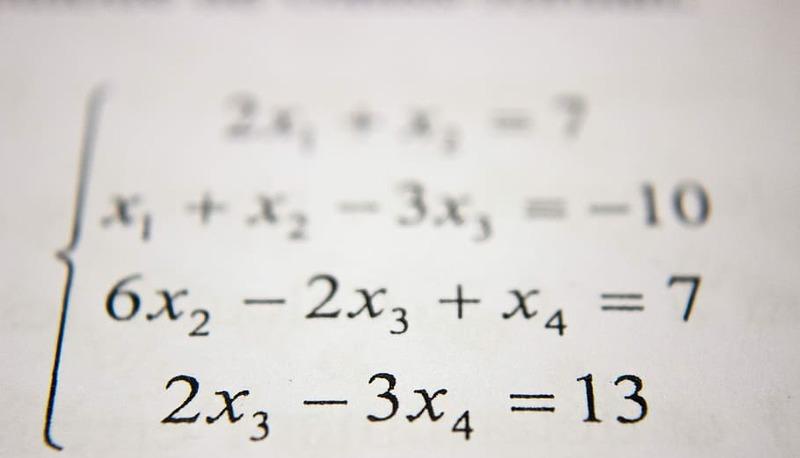
Gli intervalli
Per capire i limiti, c’è prima da prendere in analisi il concetto d’intervallo a cui esso può appartenere o meno. Un intervallo è un sottoinsieme di numeri reali e, geometricamente, corrisponde ad una semiretta (nel caso sia un intervallo illimitato) o ad una retta (intervallo limitato). Oltre a queste caratteristiche, esso può essere chiuso (se gli estremi appartengono all’intervallo) o aperto (se essi non vi appartengono). Un esempio di intervallo limitato è
Ogni intervallo ha delle caratteristiche: gli estremi (
Uno dei due estremi degli intervalli è
Gli intorni
Analizzando i punti di un intervallo, possiamo avere dei numeri classificati come “intorno”. Un intorno completo di
dove
Nel caso in cui
Gli intorni, inoltre, possono essere di due tipi:
- Destro di [math]x_0[/math]: intervallo[math]I_\delta^+ (x_0 )= ] x_0; x_0+ \delta [/math];
- Sinistro di [math]x_0[/math]: intervallo I_\delta^- (x_0 )= ] x_0- \delta; x_0 [/math] .
Vi sono anche intorni d’infinito:
- Intorno di meno infinito: un intervallo aperto illimitato inferiormente:
[math]I (-\infty) = ]-\infty ;a[ = {x \in \mathbb{R} :x<a} [/math]; - Intorno di più infinito: un intervallo aperto illimitato superiormente: [math]I (+\infty) = ] b; +\infty [ = {x \in \mathbb{R} :x>b}[/math];
- Intorno di infinito: unione tra l’intorno di [math]+\infty[/math]e di[math]-\infty[/math]ossia:[math]I (\infty)= I(-∞) \cup I(+∞)=\{x \in \mathbb{R} : x<a \vee x>b\}[/math];
- Intorno circolare di infinito: intorno di [math]x_0[/math], cioè[math]I_c (\infty)= ]-\infty; -c [\cup] c; +\infty [ [/math]con[math] c \in \mathbb{R}^+[/math].
Gli insiemi
Non tutti gli insiemi sono intervalli ma anch’essi possono essere limitati o illimitati. Un insieme numerico
- Superiormente limitato: se si può determinare un numero reale [math]M[/math](detto maggiorante di F) tale che[math]x \le M \forall x \in F[/math], se appartiene all’insieme è detto anche massimo – vi è un estremo superiore ([math]M = \text{sup} F[/math]) di F tale che:
- [math] x \le M \forall x \in F[/math]
- [math] \forall \epsilon > 0 \exists x \in F : x>M-\epsilon[/math]
- Inferiormente limitato: si può determinare un numero reale [math]m[/math](detto minorante di F) tale che[math] x \ge m \forall x \in F[/math], se appartiene all’insieme è detto anche minimo – vi è un estremo inferiore ([math]m = \text{inf} F[/math]) tale che:
- [math] x \ge m \forall x \in F[/math]
- [math]\forall \epsilon > 0 \exists x \in F : x < m+\epsilon[/math]
- Limitato : se è limitato sia inferiormente che superiormente;
- Illimitati superiormente: se esiste sempre un elemento di [math]F[/math]che è maggiore di[math]m[/math]per ogni numero reale[math]m[/math];
- Illimitati inferiormente: se esiste sempre un elemento di [math]F[/math]che è minore di[math]m[/math]per ogni numero reale[math]m[/math];
- Illimitato: se l’insieme è limitato sia superiormente che inferiormente.
Comportamento di una funzione quando tende ad un certo punto
Consideriamo la funzione
Poiché
Otteniamo che
Poiché all’avvicinarsi di
Per
Premesse ed esempio fatto, è possibile stabilire che si ha un limite finito di una funzione
Nel caso in cui
Tipi di limiti
Esistono vari tipi di limiti necessitano di una loro categorizzazione: ve ne sono per eccesso o difetto, sinistri o destri:
- Limite per eccesso : nel caso in cui [math]f(x)[/math]tende a[math]l[/math]per eccesso si scrive[math]\lim_{x \rightarrow x_0} f(x) = l^{+}[/math], e si ha la condizione[math]f(x)>l[/math];
- Limite per difetto : nel caso in cui [math]f(x)[/math]tende a[math]l[/math]si scrive[math]\lim_{x \rightarrow x_0} f(x) = l^{-}[/math], con aggiunta condizione f(x) < l;
- Limite destro: nel caso in cui un limite [math]\lim_{x \rightarrow x_0^{+}} f(x)=l[/math]si verifichi per ogni[math]x[/math]appartenente all’intorno destro di[math]x_0[/math], cioè[math]] x_0; x_0+\delta[ [/math];
- Limite sinistro: nel caso in cui un limite [math]\lim_{x \rightarrow x_0^{-}} f(x)=l[/math]si verifichi per ogni[math]x[/math]appartenente all’intorno sinistro di[math]x_0[/math], cioè[math]] x_0-\delta; x_0[ [/math].
Se, invece, i valori della funzione crescono sempre di più, si dice che la funzione diverge positivamente e tende a
Nel caso opposto, si dice che la funzione diverge negativamente. Si ha un limite
Tra le applicazioni a livello grafico dei limiti, rientra la determinazione degli asintoti, in questo caso, verticali. Se
Spostando l’ottica, su un limite finito di una funzione per
Analogamente
Proseguendo con la determinazione degli asintoti, esistono anche gli asintoti orizzontali. Se
Limiti: teoremi principali
A prescindere dal valore a cui tende
- Teorema di unicità del limite: se [math]f(x)[/math]ha limite finito[math]l[/math]per[math]x \rightarrow x_0[/math], allora tale limite è unico;
- Teorema della permanenza del segno: se il limite di una funzione per [math]x[/math]che tende a[math]x_0[/math]è un numero[math]l[/math]diverso da 0, allora esiste un intorno[math]I[/math]di[math]x_0[/math](escluso al più[math]x_0[/math]) in cui[math]f(x)[/math]e[math]l[/math]hanno lo stesso segno.
- Teorema del confronto : siano [math]h(x), f(x), g(x)[/math]tre funzioni definite in uno stesso intorno di[math]x_0[/math]– escluso al più il punto[math]x_0[/math]. Se in ogni punto di tale intorno diverso da[math]x_0[/math]risulta[math]h(x) \le f(x) \le g(x)[/math]e il limite delle due funzioni[math]h(x)[/math]e[math]g(x)[/math], per[math] x \rightarrow x_0[/math]vale in entrambi i casi[math]l[/math], allora anche il limite di[math]f(x)[/math]per[math]x[/math]che tende a[math]x_0[/math]è uguale a[math]l[/math].
Le dimostrazioni dei suddetti teoremi sono nell'allegato.
Calcolo di limiti elementari
In generale, valgono le seguenti uguaglianze:
- Se [math]f(x)=x^n[/math], allora[math]\lim_{x \rightarrow +\infty} f(x) = +\infty[/math]per ogni[math]n[/math]positivo.
Se invece[math]x \rightarrow -\infty[/math]allora il limite vale[math]-\infty[/math], mentre vale sempre[math]+\infty[/math]se[math]n[/math]è pari; - Se [math]f(x) = \sqrt[n]{x}[/math]con[math]n[/math]positivo, allora[math]\lim_{x \rightarrow 0^{+}} f(x) = 0[/math]e[math]\lim_{x \rightarrow +\infty} f(x) = +\infty[/math]. Se[math]n[/math]è dispari si può definire anche la radice nei negativi e quindi[math]\lim_{x \rightarrow -\infty} f(x) = -\infty[/math];
- Se [math]f(x)=a^x[/math]con[math]a>1[/math]allora[math]\lim_{x \rightarrow +\infty} f(x) = +\infty[/math]e[math]\lim_{x \rightarrow -\infty} f(x) = 0[/math], altrimenti se[math]0<a<1[/math]accade[math]\lim_{x \rightarrow -\infty} f(x) = +\infty[/math]e[math]\lim_{x \rightarrow +\infty} f(x) = 0[/math]. Vedremo che quest'ultima uguaglianza implica l'esistenza di un asintoto;
- Se [math]f(x)=\log_a(x)[/math]e[math]a>1[/math]allora[math]\lim_{x \rightarrow +\infty} f(x) = +\infty[/math]e[math]\lim_{x \rightarrow 0^{+}} f(x) = -\infty[/math], altrimenti se[math]0 < a < 1[/math]si avrà l'inverso, cioè[math]\lim_{x \rightarrow 0^{+}} f(x) = +\infty[/math]e[math]\lim_{x \rightarrow +\infty} f(x) = 0[/math];
Ulteriori strumenti per il calcolo dei limiti
Se ci viene richiesto di calcolare il limite per
- Limite della somma: se [math]\lim_{x \rightarrow x_0} f(x) = l[/math]e[math]\lim_{x \rightarrow x_0} g(x) = m[/math]allora[math]\lim_{x \rightarrow x_0} f(x)+g(x) = l+m[/math];
- Limite del prodotto: se [math]\lim_{x \rightarrow x_0} f(x) = l[/math]e[math]\lim_{x \rightarrow x_0} g(x) = m[/math]allora[math]\lim_{x \rightarrow x_0} f(x)g(x) = l \cdot m[/math]
- Limite di una funzione moltiplicata per una costante: possiamo dire che in generale [math]\lim_{x \rightarrow x_0} k \cdot f(x) = k \cdot \lim_{x \rightarrow x_0} f(x)[/math].
- Limite del quoziente: se [math]\lim_{x \rightarrow x_0} f(x) = l[/math]e[math]\lim_{x \rightarrow x_0} g(x) = m[/math]e[math] m \neq 0[/math]allora[math]\lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = \frac{\lim_{x \rightarrow x_0} f(x)}{\lim_{x \rightarrow x_0} g(x)}[/math].
- Limite di una funzione elevata ad un certo esponente: se [math]\lim_{x \rightarrow x_0} f(x) = l[/math], allora[math]\lim_{x \rightarrow x_0} [f(x)]^n = l^n[/math].
- Limite di una funzione elevata ad un'altra funzione: se [math]\lim_{x \rightarrow x_0} f(x) = l>0[/math]e[math]\lim_{x \rightarrow x_0} g(x) = m[/math]allora[math]\lim_{x \rightarrow x_0} [f(x)]^{g(x)} = l^m[/math].
- Limite di una funzione composta: se [math]y=f(z)[/math]e[math]z=g(x)[/math]tali che[math]f(x)[/math]sia continua in[math]z_0[/math]e[math]\lim_{x \rightarrow x_0} g(x) = z_0[/math]allora[math]\lim_{x \rightarrow x_0} f(g(x)) = f(z_0)[/math].

Forme indeterminate
Le forme indeterminate sono delle forme che si possono incontrare nel calcolo dei limiti, non ne permettono il calcolo diretto, ma è possibile arrivare alla soluzione utilizzando dei trucchetti.
Le forme indeterminate sono:
- Forma indeterminata [math]+\infty-\infty[/math]: per calcolare il limite infinito di una funzione di grado[math]n[/math]basta guardare solo il coefficiente di grado[math]n[/math].[math]\lim_{x \rightarrow +\infty} a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0 = \lim_{x \rightarrow +\infty} a_nx^n[/math]
- Forma indeterminata [math]0 \cdot \infty[/math]: si svolge la funzione moltiplicandola o dividendola per un certo valore in modo da eliminare i fattori che determinano l’indecisione.
- Forma indeterminata [math]\infty / \infty[/math]. Se il grado del numeratore è uguale al grado del denominatore allora il limite per[math]x \rightarrow \infty[/math]è uguale al rapporto tra i coefficienti di grado massimo, se invece il numeratore ha grado superiore del denominatore, il limite vale[math]\pm \infty[/math], altrimenti il limite vale[math]0[/math]. Per ulteriori informazioni su questa forma indeterminata si rimanda al file allegato, ove viene discusso degli ordini di infinito.
- Forma indeterminata [math]0^0, 1^{\infty}, \infty^{0}[/math]: in questo caso si ricorre all'identità[math]f(x)^{g(x)} = e^{g(x) \cdot \ln(f(x))}[/math]
Limiti notevoli
Così noti per essere, appunto, noti, spesso ricorrono nascosti opportunamente nel calcolo dei limiti. I principali sono:
Continuità
Per quanto riguarda le funzioni continue, anch’esse hanno dei teoremi d’applicazione. Una funzione
- È definita in [math]x0[/math]: esiste[math]f(x_0)[/math];
- Esiste limite finito [math]lim_{x \rightarrow x_0} f(x)[/math];
- Il valore del limite è uguale a f(x_0)
Se tali condizioni valgono limitatamente ad un certo intervallo
Di seguito una lista di teoremi utili nelle funzioni continue.
- Teorema di Weierstrass:, che prende in considerazione i due punti di [math]f(x)[/math]:
massimo assoluto, se esiste il punto massimo[math]M[/math]; minimo assoluto, se esiste il minimo[math]m[/math]. Stabilendo che: se[math]f[/math]è una funzione continua, allora essa assume – nell’intervallo [a; b] – il massimo assoluto e il minimo assoluto. - Il teorema dei valori intermedi procede sulla stessa linea: se f è una funzione continua in [a; b], allora essa assume tutti i valori compresi tra il massimo e il minimo.
- Il teorema di esistenza degli zeri indica che se f è una funzione continua in [a; b], e nei suoi estremi essa assume valori di segno opposto, esiste almeno un punto in cui f si annulla, cioè [math]f(c) = 0.[/math]
Discontinuità
Nel caso in cui si abbiano funzioni non continue
Si rimanda al file allegato per capire come classificare le varie discontinuità.
Per ulteriori approfondimenti sulla discontinuità, vedi anche qua
Asintoti
Una retta si definisce asintoto di una funzione, se la distanza di un punto
- Asintoti verticali: hanno equazione [math]x=x_0[/math]e si hanno quando[math]\lim_{x \rightarrow x_0} = \pm \infty[/math].
- Asintoti orizzontali: hanno equazione [math]y=l[/math]e si hanno quando[math]\lim_{x \rightarrow \pm \infty} = l [/math].
- Asintoti obliqui: hanno equazione [math]y = mx+q[/math]e si hanno quando[math]\lim_{x \rightarrow \pm \infty} \frac{f(x)}{x} = m[/math]e[math]\lim_{x \rightarrow \pm \infty} f(x)-mx = q[/math].
Per ulteriori approfondimenti sugli asintoti vedi anche qua
Cenni al grafico probabile
Rimanendo in tema, è possibile ricavare un grafico probabile seguendo 6 passi:
1) determinare il dominio; 2) studiare le (eventuali) simmetrie rispetto all’asse y o all’origine O; 3) determinare le intersezioni con gli assi; 4) studiare il segno; 5) calcolare i limiti agli estremi del dominio e studiare i punti di discontinuità; 6) determinare gli asintoti.
Il concetto di limite, quindi, serve a descrivere l'andamento di una funzione all'avvicinarsi del suo argomento a un dato valore (limite di una funzione) oppure l'andamento di una successione al crescere illimitato dell'indice (limite di una successione). I limiti si utilizzano in tutti i rami dell'analisi matematica; sono usati ad esempio per definire la continuità, la derivazione e l'integrazione.
I Limiti: tutto quello che c’è da sapere
di Pero Claudia
Per capire i limiti, c’è prima da prendere in analisi il concetto d’intervallo a cui esso può appartenere o
meno. Un intervallo è un sotto-insieme di numeri reali e, geometricamente, corrisponde ad una semiretta
(nel caso sia un intervallo illimitato) o ad una retta (intervallo limitato). Oltre a queste caratteristiche, esso
può essere chiuso (se gli estremi appartengono all’intervallo) o aperto (se essi non vi appartengono). Come
mostrato:
Esempi di intervalli limitati:
Da queste quattro tipologie si possono ricavare le caratteristiche degli intervalli: gli estremi
b−a b+a
(a, b), l’ampiezza (b – a), il raggio ( ), il centro ( ).
2 2
Esempi di intervalli illimitati:
Uno dei due estremi dei limiti è a, poiché +∞ e -∞ non sono numeri reali e sono esclusi
dall’intervallo.
Analizzando i punti di un intervallo, possiamo avere dei numeri classificati come “intorno”. Un intorno
completo di x (numero reale) è un intervallo qualunque di I (x ), così definibile:
0 0
¿ δ δ
dove e sono numeri reali, come mostrato nell’esempio:
( )
=¿ −δ + ¿
I x x ; x δ 1 2
0 0 1 0 2
=δ
δ (x )
I
Nel caso in cui , x sarà un punto medio. Si avrà che l’intervallo aperto ha un centro x
0 0
δ 0
1 2 e raggio δ – si tratta di un introno circolare, così definibile:
¿ 1
( ) =¿ −δ +δ ¿
I x x ; x
δ 0 0 0
Gli intorni, inoltre, possono essere di due tipi:
¿
( )
+¿ =¿ + ¿
x x ; x δ
1. Destro di x : intervallo ;
0 0 0
0 ¿
I δ
¿
( )
−¿ =¿ −δ ¿
x x ; x
2. Sinistro di x : intervallo .
0 0 0
0 ¿
I δ
1 Da ricordare che: l’intersezione e l’unione di più intorni completi di x sono intorni completi di x .
0 0 1
I Limiti: tutto quello che c’è da sapere
di Pero Claudia
Vi sono anche intorni d’infinito:
1. Intorno di meno infinito: un intervallo aperto illimitato inferiormente:
{ }
∈
¿ <a
x R : x ;
(−∞ )=¿−∞ ¿
I ; a { }
∈
¿ x R : x> b
2. Intorno di più infinito: un intervallo aperto illimitato superiormente: ;
( )=¿
+∞ +∞ ¿
I b ;
3. Intorno di infinito: unione tra l’intorno di -∞ e di +∞, ossia:
{ }
( )=I (−∞ ) ( )= ∈
+∞ >b
I ∞ U I x R : x< a V x ;
¿ +¿
4. Intorno circolare di infinito: intorno di x , cioè con .
[ ] ¿
( )=¿−∞ ¿ ∈
I ∞ ;−c U c ;+ ∞ c R
0 c
Non tutti gli insiemi sono intervalli ma anch’essi possono essere limitati o illimitati. Un insieme
∁
F R
numerico è detto:
Superiormente limitato: si può determinare un numero reale α (detto maggiorante di F) tale
∀ ∈
x ≤ α x F
che , se appartiene all’insieme è detto anche massimo – vi è un estremo
2
superiore (sup ) di E tale che il suo numero reale M:
E ∀ ∈
x E
3
x ≤ M , con
∀ ∃ ∈
>0 −ε)
ε x E x>( M
tale che ;
Inferiormente limitato: si può determinare un numero reale β (detto minorante di F) tale
∀ ∈
x ≥ β x F
che , se appartiene all’insieme è detto anche minimo – vi è un estremo
4
inferiore di E tale che il suo numero reale L:
∀ ∈
x E
5
x ≥ L , con
∀ ∃ ∈ )
ε>0 x E x<(L+ε
tale che ;
6
Limitato : se è contenuto da un intervallo limitato – F è limitato se il numero reale k è tale
| | ∀ ∈
x ≤k x F
che .
Un insieme numerico finito è sempre contenuto in un intervallo limitato. Tuttavia, vi sono anche altri insiemi:
Illimitati superiormente: se vi è un numero reale m rispetto cui F è maggiore, cioè
∀ ∃ ∈
m∈ R x F tale che x > m;
Illimitati inferiormente: vi è un numero reale m a cui F è inferiore,
∀ ∃ ∈
m∈ R x F
cioè tale che x < m;
Illimitati: l’insieme è limitato sia superiormente che inferiormente.
2 Se non è vuoto, oltre alle altre caratteristiche, esiste ed è sempre unico.
3 M è un maggiorante di E.
4 Se non è vuoto, oltre alle altre caratteristiche, esiste ed è sempre unico.
5 L è un minorante di E.
6 Un intervallo limitato non è un insieme finito, in quanto non è costituito da un numero finito di elementi. 2
I Limiti: tutto quello che c’è da sapere
di Pero Claudia
7
Prendendo, ora, in esame la funzione y = f(x) , come mostrata nel grafico:
Per meglio capire la funzione, consideriamo il seguente esempio, con l’obiettivo di studiarla vicino al punto
8
x = 3 :
0
2 −6
2 x x { }
( ) D=R− 3
=
y=f x , .
x−3
Poiché f(x) non è definita in 3, non è possibile considerare f(3). È necessario, quindi, studiare la funzione
tabella
quando si approssima a quel dato valore, di conseguenza diamo ad x un tot. valori che si avvicina a 3 .
x 2,9 2,99 2,999 → 3 ← 3,001 3,01 3,1
f(x) 5,8 5,98 5,998 → ? ← 6,002 6,02 6,2
Poiché all’avvicinarsi di x a 3, f(x) si avvicina a 6, se preso un qualunque valore di x in un intorno di 3
sempre minore, allora f(x) si trova in un intorno di 6 sempre minore. Esaminato attraverso un qualunque
intorno circolare, invece, di 6 di ampiezza ε I (6), vi sarà sempre un intorno di 3 i cui punti x (con x ≠ 3)
ε
avranno un’immagine di f(x) contenuta nell’intorno I (6), poiché soddisfano la disequazione
ε
| | | | | |
( )−6
−3 (
2 2 x x x−3)
(
2 x x−3)
−6
2 x x
| |
( )−6 <ε −6 <
f x ε
<ε < ε
→ → → →
x−3
x−3
x−3 | |
( ) (x−3)
2 x−6 < ε
x−3
prendendo in considerazione la condizione d’esistenza, semplifichiamo
ε ε ε
| |
| | | | < <
x−3 3− x<3+
< <
2 x−6 ε 2 x−3 ε
→ → →
2 2 2
quindi, le soluzioni della disequazione saranno i punti dell’intorno
¿ ε ε Supponendo che ε = 1, il grafico sarà così rappresentabile:
( ) =¿ ¿
I 3 3− ; 3+
2 2
7 Definita nell’insieme D e studiandola nel caso in cui i suoi valori tendano ad x – dal grafico si vede che la funzione,
0 ∉
x D
f(x) f(x )
avvicinandosi ad x , si avvicina anche ad l (che non coincide con poiché .
0
0 0
8 Poiché i punti devono essere quanto più possibile vicini ad x l’ideale sarebbe che la funzione sia definita in questi punti: x deve
0 0
punto d’accumulazione
essere un per D. 3
I Limiti: tutto quello che c’è da sapere
di Pero Claudia ( ) =6
lim f x
Per x che tende a 3, f(x) ha limite 6: .
x→ 3 9
Premesse ed esempio fatto, è possibile stabilire che si ha un limite finito di una funzione f(x) – con x
tendente ad x e, per limite, numero reale l – se si può determinare un intorno completo I di x tale che
0 0
( )=l
lim f x
| |
( )−l <
f x ε , cioè . Per essere valido, la condizione f(x) deve essere definita in tutti i punti
x → x 0 dell’intorno I(x ), escluso al più x :
0 0
| |
( ) ( )
( )=l ( )
∀ ∃ ∀ ∈
>0 −l <ε
lim f x se ε I x : f x , x I x , x ≠ x .
0 0 0
x → x 0 10
Nel caso in cui x appartenga al dominio di f e coincida anche con il limite di f(x) si dice che f è continua
0
in x . Le funzioni continue avranno un grafico la cui curva è senza interruzioni (retta o parabola). Per
0
calcolare il limite è sufficiente calcolare il valore della funzione nel punto dato – per una funzione f(x) = 2x
lim 2 x=2∗7=14 11
continua nel punto 7: . Essa, a seconda dei suoi componenti, è classificabile in:
x→ 7 =k
lim k
1. Funzione costante: f(x) = k è continua in tutto R – ;
x → x 0
2
( )=3 −2
2. Funzione polinomiale: è continua in R (generalmente sono tutte continue,
f x x x+5
specialmente le potenze di x);
{ }
∪
+¿ 0
√
3. Funzione radice quadrata: , definita in , è continua per ogni x reale positivo o
y= x ¿
R
nullo;
sin x cos x
4. Funzioni goniometriche: sono continue sia che , come anche le loro derivanti;
x
5. Funzione esponenziale: , con a > 0 è continua in tutto R;
y=a
y=log x +
6. Funzione logaritmica: , con a > 0, a ≠ 1, definita in tutto R .
a
Anche i limiti necessitano di una loro categorizzazione: ve ne sono per eccesso o difetto, sinistri o
destri: +¿ ¿
( )=l
12
Limite per eccesso : nel caso in cui f(x) tende a l per eccesso si ha un limite ,
lim f x
x → x 0
con aggiunta condizione f(x) > l;
9 Che esiste solo se esistono i suoi limiti sinistro e destro e coincidono.
10 È continua nel suo dominio D, se risulta continua in ogni punto di D.
11 Vedi pag. 5 per lo svolgimento.
12 Valido anche per x → +∞, basta considerare l’intorno di +∞. 4
I Limiti: tutto quello che c’è da sapere
di Pero Claudia −¿ ¿
( )=l
13
Limite per difetto : nel caso in cui f(x) tende ad l per difetto si ha un limite , con
lim f x
x → x 0
aggiunta condizione f(x) < l;
+¿ ( ) =l
x → x f x
0
Limite destro: nel caso in cui un limite si verifichi per ogni x appartenente
¿
lim
¿ ¿
all’intorno destro di x , cioè ;
¿ +δ ¿
x ; x
0 0 0
−¿ ( ) =l
x → x f x
0
Limite sinistro: nel caso in cui un limite si verifichi per ogni x appartenente
¿
lim
¿ ¿
all’intorno sinistro di x , cioè .
¿ −δ ¿
x ; x
0 0 0
Se, invece, i valori della funzione crescono sempre di più, si dice che la funzione f diverge positivamente
e tende a +∞. Si ha un limite +∞ per x che tende ad x se la funzione f(x) – definita in un intervallo [a; b],
o
ma non definita con x interno allo stesso intervallo – tenderà a +∞ per ogni numero reale positivo M in cui
0
è determinabile un intorno completo di I di x , tale che f(x) > M:
0
( ) ( )
( )=+ ( )>
∀ ∀ ∈
>
lim f x ∞ se M 0∃ I x :f x M , x I x , x ≠ x .
0 0 0
x → x 0
Nel caso opposto, si dice che la funzione f diverge negativamente. Si ha un limite -∞ per x che tende
ad x se una funzione f(x) – definita in un intervallo [a; b], ma non definita con x interno allo stesso
0 0
intervallo – tenderà a -∞ per ogni numero reale positivo M in cui è determinabile un intorno completo I di x ,
0
tale che f(x) < M:
( ) ( )
( )=−∞ ( )
∀ ∃ ∀ ∈
>0 <
lim f x se M I x : f x M , x I x , x ≠ x .
0 0 0
x → x 0
Prendendo in considerazione sia una funzione divergente positivamente che una negativamente, è
( )=∞
lim f x
possibile dire che non esiste un limite, ad esempio, per x → 0: .
x → x 0 14
Tra le applicazioni a livello grafico dei limiti, rientra la determinazione degli asintoti , in questo caso,
( ) =+∞
lim f x ,−∞ oppure ∞
verticali. Se allora si ha che x = c è un asintoto verticale, che possono
x→ c essere anche infiniti.
Spostando l’ottica, su un limite finito di una funzione per x che tende a +∞, i valori di x saranno sempre
maggiori, superando un qualunque numero reale positivo c. Si ha una funzione f(x) – definita in un
intervallo illimitato a destra – che tende al numero reale l per x tendente a +∞, quando si può determinare
| |
( )=l ( )−l
∀ ∃c ∀
> >0 < >c
lim f x se ε 0 : f x ε , x
| |
( )−l ∈
<
f x ε per ogni x I
un intorno I di +∞ tale che : .
x →+∞
Con un limite finito di una funzione con x che tende a -∞, in questo caso, si ha una funzione f(x) –
definita in un intervallo illimitato a sinistra – con limite reale l per x tendente a -∞, quando si può trovare un
| |
( )−l ∈
<
f x ε per ogni x I
intorno I di -∞ tale che :
| |
( )=l ( )−l
∀ ∃ ∀
>0 <ε
lim f x se ε c>0 : f x , x← c .
x →−∞
Entrami i casi possono essere sintetizzati se si considera un intorno di ∞ determinato dalle x per le quali |x|
x<−c V x> c
> c, ossia , con c numero reale casuale.
13 Valido anche per x → -∞, basta considerare l’intorno di -∞.
14 Vedi pag. 5
I Limiti: tutto quello che c’è da sapere
di Pero Claudia ( )=q
lim f x
Proseguendo con la determinazione degli asintoti, quelli orizzontali, i oppure
x →+∞
( )=q ( )=q
lim f x lim f x
o, ancora, allora si ha che y = q, che è un asintoto orizzontale. Esso può
x →−∞ x→∞
essere destro o sinistro ed inoltre, la distanza di un punto P da un asintoto orizzontale tende a 0 quando x
tende a +∞, -∞, ∞.
Una funzione per x →+∞ diverge positivamente in due casi:
1. Limite +∞ di una funzione per x che tende a +∞, se in una funzione f(x) – definita in un intervallo
illimitato a destra per x che tende a +∞ –si può definire un intorno I di +∞ per ogni numero reale
positivo M:
( )=+∞ ( )
∀ ∃c ∀
>0 >0 > >c
lim f x se M : f x M , x ;
x →+∞
2. Limite +∞ di una funzione per x che tende a -∞, se in una funzione f(x) – definita in un intervallo
illimitato a sinistra per x che tende a -∞ – si può definire un intorno I di -∞ per ogni numero reale
positivo M:
( )=+ ( )
∀ ∀
> >0 >
lim f x ∞ se M 0∃ c :f x M , x← c .
x →−∞








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









