Determina l'insieme di definizione e quindi risolvi in
[math]RR[/math]
la seguente equazione:
[math]1/(x^2-5x+6)+1/(x^2-4x+3)-1/(x^2-3x+2)=0[/math]
[math]1/(x^2-5x+6)+1/(x^2-4x+3)-1/(x^2-3x+2)=0[/math]
;
Il m.c.m. è
[math](x^2-5x+6)(x^2-4x+3)(x^2-3x+2)[/math]
, quindi
[math]((x^2-4x+3)(x^2-3x+2)+(x^2-5x+6)(x^2-3x+2)-(x^2-5x+6)(x^2-4x+3))/((x^2-5x+6)(x^2-4x+3)(x^2-3x+2))=0[/math]
Affinchè l'equazione abbia significato dobbiamo porre il denominatore diverso da zero,
ottenendo così l'insieme di definizione dell'equazione.
[math](x^2-5x+6)(x^2-4x+3)(x^2-3x+2)!=0[/math]
Studiamo singolarmente le tre
equazioni di secondo grado 1)
[math]x^2-5x+6!=0[/math]
[math]Delta=b^2-4ac=(-5)^2-(4 \cdot 1 \cdot 6)=25-24=1[/math]
[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(5+-1)/2 => x_1!=3 ^^ x_2!=2[/math]
.
2)
[math]x^2-4x+3!=0[/math]
[math](Delta)/4=(b/2)^2-ac=(-2)^2-(3 \cdot 1)=4-3=1[/math]
[math]x_(1,2)=(-b/2+-\sqrt{(Delta)/4})/a=(2+-1) => x_1!=3 ^^ x_2!=1[/math]
.
3)
[math]x^2-3x+2!=0[/math]
[math]Delta=b^2-4ac=(-3)^2-(4 \cdot 1 \cdot 2)=9-8=1[/math]
[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(3+-1)/2 => x_1!=1 ^^ x_2!=2[/math]
.
In definitiva l'equazione è risolvibile per
[math]x!=1,x!=2,x!=3[/math]
.
Ora possiamo moltiplicare ambo i membri per
[math](x^2-5x+6)(x^2-4x+3)(x^2-3x+2)[/math]
e otteniamo:
[math](x^2-4x+3)(x^2-3x+2)+(x^2-5x+6)(x^2-3x+2)-(x^2-5x+6)(x^2-4x+3)=0[/math]
;
Raccogliamo i termini simili
[math](x^2-4x+3+x^2-5x+6)(x^2-3x+2)-(x^2-5x+6)(x^2-4x+3)=0[/math]
;
[math](2x^2-9x+9)(x^2-3x+2)-(x^4-4x^3+3x^2-5x^3+20x^2-15x+6x^2-24x+18)=0[/math]
;
[math]2x^4-9x^3+9x^2-6x^3+27x^2-27x+4x^2-18x+18-x^4+9x^3-29x^2+39x-18=0[/math]
Raccogliamo i termini simili e semplifichiamo, cosi da ottenere:
[math]x^4-6xì3+11x^2-6x=0[/math]
;
[math]x(x^3-6x^2+11x-6)=0[/math]
;
Una soluzione sarà
[math]x=0[/math]
. Ora studiamo per quali valori di
[math]x[/math]
è verificata l'equazione
[math]x^3-6x^2+11x-6=0[/math]
Applichiamo il metodo di Ruffini:
[math]P(1)=1-6+11-6=0[/math]
, pertanto
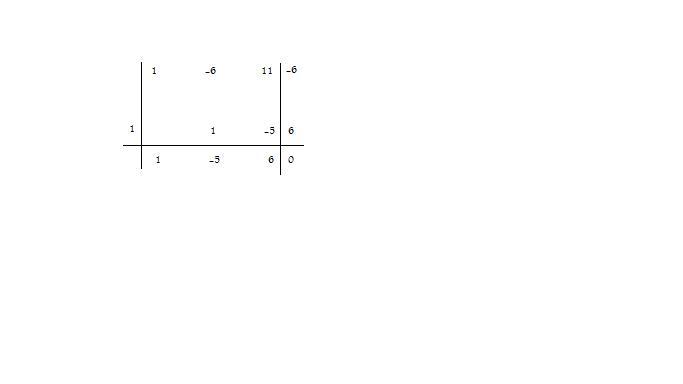
[math](x^3-6x^2+11x-6)=(x-1)(x^2-5x+6)=0[/math]
;
Questa equazione è verificata per
[math]x=1 vv x=2 vv x=3[/math]
(come visto sopra)
Ma tutte queste soluzioni non appartengono all'insieme di definizione,
pertanto l'unica soluzione accettabile sarà:
[math]x=0[/math]
.
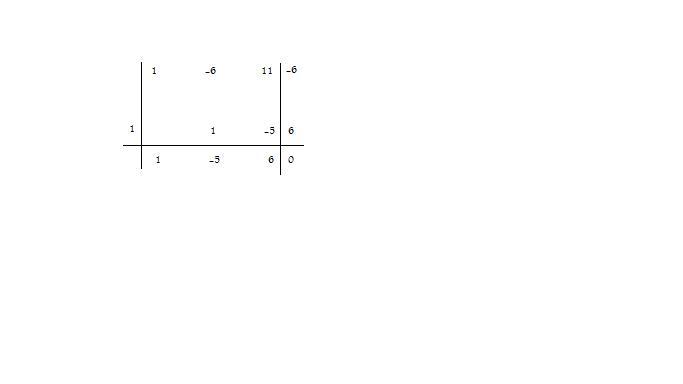






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo