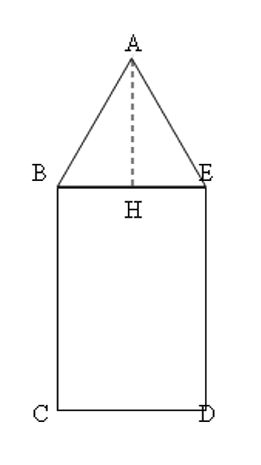
Il poligono in figura si compone di un rettangolo e di un triangolo equilatero di lato 14cm. Calcola l'area del poligono sapendo che il suo perimetro è di 92cm.
Dati noti
[math]AB=AE=BE=CD=14cm[/math]
[math]2p=92cm[/math]
Dati da ricavare
[math]Area(ABCDE)[/math]
Svolgimento
Dal perimetro togliamo i lati AB, AE, CD rimangono i lati BC e ED che sono uguali, quindi
[math]BC=(2p-14-14-14)/2 cm=(92-42)/2 cm = 25cm[/math]
L'area del rettangolo è
[math]14 \cdot 25cm^2 = 350cm^2[/math]
Per ricavare l'area del triangolo equilatero ABE ricaviamo la misura dell'altezza AH per mezzo della formula
[math]AH=\sqrt{3}/2 \cdot 14cm=12,12cm[/math]
Area del triangolo
[math]1/2 14 \cdot 12,12 cm^2=84,84cm^2[/math]
Area del poligono
[math]350cm^2 + 84,84cm^2 = 434,84cm^2[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
