Circonferenza, cerchio e corda: definizioni, differenze e proprietà

In quest'appunto troverai le definizioni di cerchio, circonferenza, arco, corda, diametro e una breve ricapitolazione delle proprietà dei poligoni inscritti, degli angoli al centro e degli angoli alla circonferenza.

Cos'è il cerchio e qual è la differenza tra cerchio e circonferenza

Per comprendere la differenza tra cerchio e circonferenza bisogna introdurre il concetto di perimetro e di superficie. Queste due quantità possono essere definite per ogni figura piana e in particolare:

• il perimetro è il contorno di una figura. Nel caso di un poligono (cioè di una figura piana delimitata da una spezzata chiusa) esso equivale alla somma della lunghezza dei lati
• la superficie, ossia la parte di piano racchiusa all'interno del perimetro

Queste definizioni si possono estendere al cerchio, anche se quest'ultimo non è un poligono e quindi non è possibile definire dei lati. In questo caso, il perimetro è una curva chiusa che prende il nome di circonferenza. Il cerchio, invece, comprende sia la circonferenza che la superficie in essa racchiusa.

In altre parole:

• la circonferenza è una linea curva chiusa, formata da punti del piano equidistanti da un punto detto centro
• si definisce semicirconferenza la metà di una circonferenza, delimitabile attraverso un diametro
• il cerchio è una parte di piano definita da una circonferenza e da tutti i punti interni a essa

Definito un punto del piano, questo può essere intersecato da infinite circonferenze. Se, invece, fissiamo tre punti sul piano, essi verranno tutti intersecati da una e una sola circonferenza.

Differenza tra diametro, corda e arco

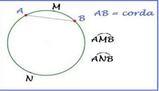
Come abbiamo già anticipato, in un cerchio vi è la superficie (la parte di piano racchiusa) e la circonferenza (il contorno che la racchiude). La circonferenza è fatta di infiniti punti: se ne uniamo due attraverso un segmento possiamo ottenere un diametro o una corda.

Se questo segmento non passa per il centro della circonferenza prende il nome di corda. Se, invece, il segmento interseca il centro della circonferenza si definisce diametro. La lunghezza del diametro è pari al doppio del raggio, ossia al doppio della distanza di tutti i punti della circonferenza dal centro.

Per quanto riguarda l'arco, invece, esso non è altro che una parte della circonferenza, ossia un "pezzo" della curva che racchiude la superficie.

Poligoni inscritti: alcune proprietà relative a triangoli e quadrilateri inscritti

In geometria, le figure piane possono essere inscritte o circoscritte. Una figura si dice inscritta quando i vertici appartengono alla circonferenza. Sono, invece, circoscritti, i poligoni cui lati sono tangenti alla circonferenza inscritta al suo interno. Alcuni poligoni particolari presentano delle proprietà quando sono inscritti, ed esse sono utili a valutare i loro lati o angoli senza fare alcun calcolo.

Un triangolo qualsiasi è sempre inscrivibile a una circonferenza, dal momento che per tre punti del piano passa una sola circonferenza. Se il triangolo è inscritto in una semicirconferenza, allora esso risulta rettangolo e la sua ipotenusa coincide con il diametro della circonferenza. Vale anche il contrario: un triangolo rettangolo inscritto in una circonferenza ha la proprietà che la sua ipotenusa coincide con il diametro. Un quadrilatero è inscrivibile in una circonferenza se e solo se gli angoli opposti del quadrilatero sono supplementari.

Cosa sono gli angoli alla circonferenza e al centro e come si definiscono

Se su una circonferenza di centro

fissiamo una corda di estremi

, l'angolo

viene detto angolo al centro insistente sull'arco

. Preso un qualsiasi punto

sulla circonferenza ma al di fuori dell'arco, l'angolo

viene detto angolo alla circonferenza insistente sull'arco

. Si dice, inoltre, che l'angolo è "sotteso" all'arco. In particolare sono valide le due seguenti proprietà:

• [math]A\hat{O}B=2A\hat{C}B[/math]
• per ogni coppia di punti
  [math]C\not=C'[/math]
  si ha
  [math]A\hat{C}B=A\hat{C'}B[/math]
  tutti gli angoli alla circonferenza insistenti sullo stesso arco hanno uguale ampiezza

Gli angoli alla circonferenza sono sempre convessi (ossia non contengono i prolungamenti dei propri lati) e hanno sempre vertice sulla circonferenza e lati tangenti o secanti a quest'ultima. Un angolo al centro ha vertice nel centro della circonferenza e può essere concavo, convesso o piatto. Questo dipende dalla lunghezza dell'arco su cui l'angolo al centro insiste, cioè l'arco delimitato dall'intersezione tra le semirette dell'angolo e la circonferenza:

• se questo insiste su un arco più ampio della semicirconferenza, l'angolo contiene i prolungamenti delle semirette e quindi è concavo
• se invece l'arco su cui insiste coincide con la circonferenza risulta piatto
• se, infine, l'arco su cui insiste ha una lunghezza minore della semicirconferenza, l'angolo non contiene i prolungamenti dei lati ed è quindi convesso

Formule utili per il calcolo di superficie, circonferenza e diametro del cerchio

Per svolgere correttamente i problemi di geometria relativi al cerchio è opportuno conoscere le formule fondamentali, cioè quelle adibite al calcolo della circonferenza (impropriamente chiamata anche perimetro), della superficie e del diametro.
Indicato con

il raggio della circonferenza, con

il suo diametro, con

il perimetro e con

la superficie del cerchio, si ha che:

Per ulteriori approfondimenti sul cerchio vedi anche qui