Cerchio e circonferenza - Definizioni e proprietà

In questo appunto vengono presentate le definizioni e proprietà principali riguardanti la figura geometrica del cerchio, e quindi della sua circonferenza, raggio, diametro, corda.

Definizione di circonferenza

La circonferenza è un luogo geometrico formato da un insieme di punti che godono tutti della stessa proprietà ovvero che tutti i punti sono equidistanti da un dato punto definito come centro della circonferenza.

Definizione di Cerchio

Il cerchio è la superficie delimitata dalla circonferenza, o meglio definita come quella parte di piano delimitata appunto dalla circonferenza. Il cerchio, in quanto parte del piano, è una figura geometrica che possiede un'area e un perimetro
Il perimetro del cerchio non è altro che la lunghezza della circonferenza stessa.

per approfondimenti sul calcolo del perimetro di altre figure geometriche, vedi qui

Definizione del Centro della circonferenza

Dunque è possibile definire il centro della circonferenza come il punto fisso che si trova al centro ed è l'origine del cerchio e viene indicato con la lettera O cioè origine.

Definizione di Raggio e Diametro

In una circonferenza e dunque in un cerchio è possibile definire il concetto di raggio e di diametro . Di seguito alcune definizioni fondamentali:

• Il raggio è definito come il segmento che permette di costruire la circonferenza. Nello specifico, il raggio è il segmento che va a congiungere il centro del cerchio con qualsiasi punto della circonferenza.
• Il diametro invece è definito come il segmento che passa per il centro della circonferenza ed è formato da due volte la dimensione del raggio della circonferenza e i suoi due punti si trovano opposti sulla circonferenza.

Definizione di Corda e Arco

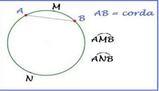
In una circonferenza e dunque in un cerchio è possibile definire il concetto di corda e di arco. Di seguito alcune definizioni fondamentali:

• La corda è un segmento che unisce due punti distinti e opposti sulla circonferenza. Da qui si può concludere che il diametro è anche una corda della circonferenza
• L'arco è una parte di circonferenza delimitata da due punti, quindi individuata a partire dalla corda.
• Una corda divide il cerchio in due segmenti circolari. Dei due segmenti uno contiene il centro e l'altro no. Il diametro infatti va a dividere il cerchio in due semicerchi distinti ma uguali (in termini di area e parte del piano delimitata).
• Due raggi dividono il cerchio in due settori circolari.
• Due circonferenze concentriche, ovvero due circonferenze che possiedo lo stesso centro, considerate però possedenti un raggio diverso, individuano una corona circolare.

Formule del cerchio

In quanto figura piana è possibile individuare alcune formule matematiche fondamentali che permettono di descrivere le caratteristiche matematiche e geometriche principali del cerchio.
Il diametro di un cerchio è pari a due volte il raggio dello stesso. Il diametrosi può esprimere attraverso la seguente relazione matematica:

• dove d è il diametro del cerchio ed r è il raggio del cerchio.

Il raggio di un cerchio è pari alla metà del diametro dello stesso. Il raggio si può esprimere attraverso la seguente relazione matematica:

Il perimetro del cerchio è individuale dalla seguente relazione matematica. Il perimetro si può esprimere attraverso la seguente relazione matematica:

• dove P è il perimetro del cerchio ed
  [math]\pi[/math]
  è il numero PiGreco.

L'area del cerchio è pari al prodotto tra il raggio al quadrato per il pigreco. L'area del cerchio si può esprimere attraverso la seguente relazione matematica:

• dove A è l'area del cerchio.

Per approfondimenti sul calcolo dell'area del cerchio vedi qui

Dalle formule fondamentali è possibile ottenere le cosiddette formule inverse.
Conoscendo l'area del cerchio è possibile ottenere il diametro e il raggio del cerchio:

Conoscendo il perimetro ì del cerchio è possibile ottenere il diametro e il raggio del cerchio:

Equazione della circonferenza noti centro e raggio

Considerando una circonferenza di cui sono noti il suo centro e il suo raggio, è possibile andare ad individuare l'equazione matematica che permette di posizionare sul piano la circonferenza. L'equazione della circonferenza nel piano è la seguente:

• dove
  [math]x_c, y_c[/math]
  sono le coordinate del punto del centro della circonferenza.

Una circonferenza centrata nell'origine ha la seguente equazione nel piano:

Proprietà della circonferenza con rette e angoli

Di seguito alcune proprietà fondamentali del cerchio e della circonferenza:

• Considerati tre punti non allineati, attraverso questi passa una ed una sola circonferenza.
• Una corda qualsiasi avrà una lunghezza sempre più piccola rispetto il diamtero, poichè esso risulta la corda massimale del cerchio
• In presenza di un poligono regolare è possibile andare a definire sempre una circonferenza, e quindi un cerchio circoscritto e inscritto alla figura stessa.

Un cerchio in quanto figura piana può entrare in contatto con i concetti di angoli e rette. Di seguito alcune proprietà fondamentali tra circonferenza e rette sul piano e circonferenza e angoli sul piano.

Circonferenze e rette sul piano

Di seguito vengono riportate alcune proprietà fondamentali che esistono tra la circonferenza e una retta sul piano:

• Una retta è secante quando ha due punti in comune con la circonferenza.
• Una retta è tangente quando ha un punto in comune con la circonferenza.
• Una retta è esterna quando non ha nessun punto in comune con la circonferenza.
• Due circonferenza sono secanti quando hanno due punti in comune.
• Due circonferenze sono tangenti quando hanno un punto in comune.
• Due circonferenze sono esterne o interne quando non hanno nessun punto in comune.
• Due rette sono sovrapposte ovvero sono concentriche e hanno lo stesso raggio

Angoli al centro e alla circonferenza

Di seguito vengono riportate alcune proprietà fondamentali che esistono tra gli angoli al centro e una circonferenza sul piano:

• Si chiama angolo al centro un angolo che ha per vertice il centro della circonferenza e per lati due raggi e i loro prolungamenti.
• Si chiama angolo alla circonferenza un angolo che ha per vertice un punto sulla circonferenza e per lati due corde e i loro prolungamenti.
• L'angolo alla circonferenza è la metà del l'angolo al centro che insiste sullo stesso arco.
  Poiché questo è valido per tutti gli angoli alla circonferenza, tutti gli angoli alla circonferenza che insistono sullo stesso arco hanno la stessa ampiezza.