Concetti Chiave
- Il formalismo matematico di Hilbert mirava a dimostrare la coerenza dell'aritmetica per fondare tutta la matematica su basi interne, prive di riferimenti esterni.
- Il principio di indeterminazione di Heisenberg sfida la causalità classica, affermando l'impossibilità di misurare simultaneamente velocità e posizione di una particella.
- La macchina di Turing, teorizzata da Alan Turing, rappresenta un modello teorico per eseguire calcoli e manipolare simboli, anticipando la logica dei moderni calcolatori.
- La discussione sulla possibilità di costruire macchine intelligenti coinvolge argomenti come il test di Turing e la critica di Wittgenstein sul linguaggio come gioco sociale.
- Nonostante i progressi tecnici, come la vittoria di Deep Blue su Kasparov, le macchine non hanno ancora superato i limiti nella comprensione semantica e nelle traduzioni linguistiche.
| Alan Turing  Ludwig Wittgenstein   E. Schrödinger; J.B.S. Il principio di indeterminazioneHaldane Il [/url]formalismo fa capo al matematico Hilbert che dal 1904 si era proposto di stabilire la coerenza dell'aritmetica, poiché tutta la matematica, geometria e fisica comprese, era riconducibile all'aritmetica. Dimostrare la coerenza interna dell'aritmetica avrebbe significato fondare l'intera matematica su se stessa, senza bisogno di fare riferimento a concetti esterni alla matematica stessa. I formalisti, infatti, considerano segni e simboli svuotati da ogni contenuto o significato. Il principio di indeterminazione è stato formulato dal fisico Heisemberg , nobel per la fisica nel 1932. 
Contraddizione con la causalità classicaSecondo questo principio è impossibile misurare contemporaneamente la posizione e la velocità di una particella. Questo principio contraddice quello classico di causalità, la cui formulazione sostiene che se si conosce lo stato attuale di un sistema isolato è possibile prevedere esattamente lo stato futuro del sistema. Macchina di Turing 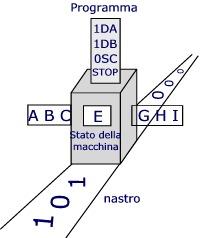 Esemplificazione di come la machina di Turing esegue 1+2. La macchina inizia con un nastro che su tutti i riquadri riporta il simbolo 0. Colloca prima un 1 e poi una sequenza di due 1, separandoli da uno 0. Il programma è il seguente
| John L. Casti I cinque di Cambridge  J. L. Casti, in questo lavoro di 'fiction scientifica', utilizza un originale metodo narrativo per esporre lo stato delle ricerche sull'intelligenza artificiale (IA) alla metà del secolo. La finzione narrativa è una serata di buona cucina e buona cultura in un elegante alloggio del Christ's College di Londra . Organizzatore dell'incontro C.P. Snow , fisico e romanziere, che ha cercato di colmare la mancanza di comunicazione tra la cultura umanistica e quella scientifica. La cena avviene nel giugno del 1949. Ospiti illustri, in ordine di arrivo: J.B.S. Haldane studioso di genetica delle popolazioni attraverso la statistica, L.Wittgenstein , i cui contributi nel campo dei fondamenti della matematica e della filosofia del linguaggio avevano fissato dei paletti significativi, nonostante fosse stato autore di due teorie del linguaggio fondamentalmente in contrasto tra di loro, elaborate in momenti distinti della sua vita, E. Schödinger , uno dei fisici più in vista del momento e tra i principali autori della teoria quantistica della materia, nel 1933 aveva ricevuto il premio Nobel per la fisica, A. Turing , autore nel 1936 di una macchina teorica, nota con il suo nome, che anticipava la struttura logica degli attuali calcolatori, durante la seconda guerra mondiale aveva avuto il compito di decifrare codici segreti dei tedeschi. I risultati ottenuti lo inducono a pensare di realizzare una machina calcolatrice in grado di duplicare, se non superare, i processi cognitivi della mente umana. Argomento della serata è una discussione logico-filosofica sulla possibilità di costruire una macchina intelligente di questo tipo. L'antefatto storico, punto di partenza della discussione è la cosiddetta prova di Gödel. Fino agli anni venti, i matematici, in particolare i formalisti , credevano nell'esistenza di un'unica logica che garantisce la verità di ogni proposizione matematica ma K. Gödel, in un lavoro del 1931, aveva dimostrato che non tutti i quesiti matematici possono avere una risposta del tipo vero o falso, conseguentemente aveva dimostrato che nessun sistema logico può dimostrare la propria coerenza, matematica compresa, e quindi aveva affossato ogni speranza di fondare la matematica su se stessa e su basi puramente logiche. Ora, si chiede Snow , è possibile ottenere una prova logica altrettanto forte che ci dica sin da subito che non è possibile costruire una macchina intelligente come l'uomo? Una tale prova renderebbe inutile avviare un programma di ricerca in questa direzione. Schödinger avverte che il principio di indeterminazione alla base della meccanica quantistica dell'elettrone non ha nulla a che vedere con la questione del libero arbitrio della mente umana, nonostante sia evidente che l'attività del cervello avviene sotto forma di movimenti di elettroni. Wittgenstein è fermamente convinto dell'assurdità della questione posta: una tale macchina non può essere costruita. Le sue argomentazioni si sviluppano grosso modo così. L'intelligenza si manifesta attraverso il linguaggio, il quale contrariamente a quanto aveva esposto nella sua prima teoria, non ha un fondamento puramente logico comune a tutte le menti umane, ma è un gioco le cui regole vengono stabilite dalla società. Turing sostiene che ogni pensiero si esprime per mezzo del linguaggio e il linguaggio per mezzo di parole, ogni parola può essere trasformata e codificata in una sequenza di simboli che una macchina può manipolare. Espone quindi il funzionamento della famosa macchina di Turing , come essa può eseguire la somma 1+2. Wittgenstein replica: la macchina di Turing sa eseguire solo calcoli pratici, forse un giorno sarà in grado di aiutare un fisico o un ingegnere ma non sarà mai in grado di raggiungere il senso di parole come intenzione, volontà, speranza , parole che traggono significato da un gioco linguistico di tipo sociale. E' vero che il linguaggio si presenta in forma simbolica ma nessun rimescolamento sintattico di simboli potrà mai raggiungere la semantica e quindi il significato dei simboli. Una macchina in grado di manipolare sintatticamente simboli non sarà mai in grado di pensare, poiché il significato delle parole risiede esclusivamente nella pratica sociale non nella logica. La concezione del linguaggio che ha Turing è simile a quella proposta da Wittgenstein nella sua prima teoria. Il linguaggio e la realtà hanno una forma logica comune, quindi il linguaggio rispecchia il mondo e le proposizioni linguistiche raffigurano i fatti del mondo. La realtà viene proiettata nelle proposizioni, perché il mondo reale e il linguaggio hanno una struttura logica comune. Ma ora Wittgenstein è convinto che la relazione tra i fatti e la loro espressione nel linguaggio non può essere espressa dallo stesso linguaggio, il quale non può essere il riflesso di una logica universale. In conclusione, il linguaggio non ha una struttura logica universale che possa essere trasferita a una macchina. Turing espone un'altra delle sue brillanti idee, il cosiddetto test di Turing . Come si fa a decidere se un altro essere umano sta pensando? Possiamo solo giudicare in base al comportamento del nostro interlocutore. Io dico o faccio qualcosa, l'interlocutore reagisce, io reagisco alla sua risposta e così via. Dopo una sequenza di interazioni di questo tipo decido se il mio interlocutore è in grado di pensare. Per stabilire se una macchina è in grado di pensare, si può eseguire il seguente esperimento. Una persona è in una stanza, la macchina in un altra. I due comunicano attraverso una porta, se dopo qualche ora di dialogo la persona non riesce a distinguere se sta comunicando con un altro uomo o con una macchina si può concludere che la macchina è intelligente quanto l'uomo. E' vero, aggiunge Turing che una macchina può eseguire soltanto le istruzioni che gli abbiamo dato ma non possiamo mai prevedere tutte le conseguenze di quelle istruzioni, se fatte eseguire un numero elevato di volte. A conclusione della serata ognuno rimane sulle proprie posizioni e Snow rimane con i suoi dubbi: cosa scrivere nel rapporto da inviare al ministro per il finanziamento delle ricerche sull'intelligenza artificiale? La questione, dopo cinquant'anni, è ancora aperta, anche se dal punto di vista tecnico la macchina ha fatto grandi passi. Nel 1997 il campione mondiale di scacchi Kasparov viene sconfitto da una macchina, Deep Blue II. Oggigiorno, un calcolatore casalingo con un discreto programma può batterci senza difficoltà. Limitatamente al gioco degli scacchi, la macchina ha superato il test di Turing. Lo stesso Kasparov ha ammesso di aver combattuto contro una forma di intelligenza aliena. La stessa cosa non può dirsi per i programmi traduttori da una lingua a un'altra: i risultati sono apprezzabili ma le traduzioni fatte dal computer si riconoscono facilmente, sono 'meccaniche'. Per avere un'idea dello stato attuale della ricerca nel campo dell'intelligenza artificiale l'autore propone i seguenti testi, disponibili anche in italiano. Searle, Mente, cervelli e intelligenza , Bompiani, Milano, 1988. Penrose, La mente nuova dell'imperatore, Rizzoli, Milano, 1992. Antonio Bernardo Su Internet [url=http://www.turing.org.uk/turing/]http://www.turing.org.uk/turing/ |
Domande da interrogazione
- Qual è il ruolo del formalismo nella matematica secondo Hilbert?
- Cosa afferma il principio di indeterminazione di Heisenberg?
- Come funziona la macchina di Turing nell'eseguire calcoli?
- Qual è la posizione di Wittgenstein sulla possibilità di costruire una macchina intelligente?
- In che modo il test di Turing valuta l'intelligenza di una macchina?
Il formalismo, secondo Hilbert, mira a stabilire la coerenza dell'aritmetica, poiché tutta la matematica può essere ricondotta ad essa, cercando di fondare la matematica su se stessa senza riferimenti esterni.
Il principio di indeterminazione di Heisenberg afferma che è impossibile misurare contemporaneamente la posizione e la velocità di una particella, contraddicendo il principio classico di causalità.
La macchina di Turing esegue calcoli manipolando simboli su un nastro, come dimostrato nell'esempio della somma 1+2, dove sostituisce simboli e si sposta tra stati predefiniti.
Wittgenstein ritiene che una macchina non possa mai raggiungere il significato delle parole, poiché il linguaggio è un gioco sociale e non può essere ridotto a una logica universale trasferibile a una macchina.
Il test di Turing valuta l'intelligenza di una macchina attraverso un dialogo tra una persona e la macchina; se la persona non riesce a distinguere se sta comunicando con un umano o una macchina, la macchina è considerata intelligente quanto l'uomo.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
