Concetti Chiave
- Il libro di Giorgio Tomaso Bagni esplora episodi storici legati a matematici del passato, offrendo un contesto temporale e geografico dettagliato.
- Ogni capitolo del libro include brani antologici e attività di laboratorio per arricchire l'esperienza didattica.
- Vengono discussi temi matematici fondamentali, tra cui il papiro di Rhind, i numeri irrazionali di Ippaso e il crivello di Eratostene.
- Il testo copre anche scoperte matematiche moderne, come il teorema di Fermat e la dimostrazione di Wiles, oltre alla geometria analitica di Descartes.
- Viene esplorato il contributo di matematici come Newton, Cantor e Russell, con particolare attenzione a problemi di calcolo e paradossi.
Giorgio Tomaso Bagni, Matematici, Antilia, Treviso, 2000, lire 27.000 Giorgio Tomaso Bagni ci propone alcuni episodi ispirati alla vita e alle ricerche di alcuni matematici del passato. Ogni episodio è collocato storicamente e geograficamente per mezzo di un asse temporale e di una cartina. Il libro propone diversi spunti didattici; in particolare, ogni capitolo è corredato di brani antologici e attività di laboratorio. In sintesi gli argomenti di alcuni capitoli del libro.
Indice
Episodi storici di matematica
All'alba: un'ipotetica ricostruzione del significato di alcune tacche, raggruppate a cinquine, incise su ossa di lupo, risalenti al 35.000 a.C. Ahmes: alcuni contenuti del più importante documento della matematica egizia, il papiro di Rhind, risalente al 1700 a.C. Talete (600 a.C.): il delicato passaggio della conoscenza matematica come forma di magia a una forma di conoscenza più complessa, espressione della razionalità intesa come deduzione logica. Ippaso (500 a.C.): la scoperta degli irrazionali. Zenone (400 a.C.): il paradosso di Achille e la tartaruga e quindi le problematiche relative all'infinito e agli infinitesimi.
Euclide (300 a.C.): i numeri primi sono infiniti. Archimede (200 a.C.): i grandi numeri espressi in notazione esponenziale. Erastone (200 a.C.): il crivello di Eratostene per determinare i numeri primi fino a un numero assegnato.
Il crivello di Eratostene
| Tabella dei numeri da 1 a 100 | Si eliminano i multipli di 2 |
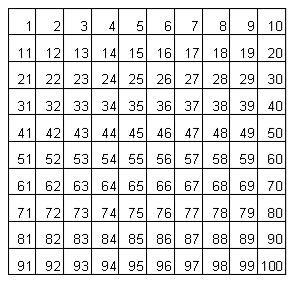 | 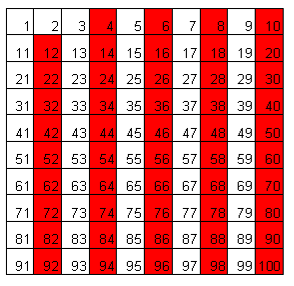 |
| si eliminano anche i multipli di 3 | si eliminano anche i multipli di 5 |
 | 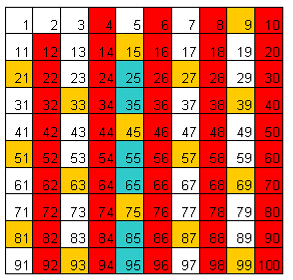 |
| si eliminano anche i multipli di 7 | i numeri rimanenti sono i numeri primi da 1 a 100 |
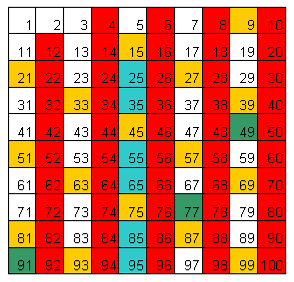 | [img alt=" " width="292" height="285"]https://cdn.skuola.net/news_foto/staticimages/libri/matematici/crivello06.
Bhaskara e i numeri immaginarigif[/img] |
Bhaskara (1100 d.C.): i misteri dello 0 e delle operazioni con lo 0. Bombelli (1500): le operazioni con i numeri immaginari
| P iù via più dimeno, fa più di meno | + per i = i |
| Meno via più di meno, fa meno di meno | - per i = i |
| Più via meno di meno, fa meno di meno | + per -i = -i |
| Meno via meno di meno, fa più di meno | - per -i = +i |
| Più di meno via più di meno, fa meno | i per i = - |
| Più di meno via men di meno, fa più | i per -i = + |
| Meno di meno via più di meno, fa più | -i per +i = + |
| Meno di meno via men di meno, fa meno | -i per -i = - |
9+16=25 che è un quadrato 25+144=169 che è un quadrato ......................................... 8+27=35 che non è un cubo 27+64=91 che non è un cubo 8+64=72 che non è un cubo .........................................
Fermat e la sua dimostrazione16+81=97 che non è una quarta potenza 81+256=337 che non è una quarta potenza 16+256=272 che non è una quarta potenza | E' impossibile separare un cubo in due cubi o un biquadrato in due biquadrati o in generale una qualsiasi potenza di grado maggiore di due in potenze dello stesso grado. |
| Ho trovato una dimostrazione veramente meravigliosa di ciò, che questo margine è troppo piccolo per contenere |
Gauss e la somma dei numeri
Gauss (1800): il singolare episodio che lo aveva visto protagonista nella scuola elementare
| La somma dei numeri interi da 1 a 100 è data da 101 per 50 = 5050 infatti
|
Domande da interrogazione
- Qual è l'obiettivo principale del libro di Giorgio Tomaso Bagni?
- Quali sono alcuni dei temi matematici trattati nel libro?
- Come viene presentata la scoperta degli irrazionali nel libro?
- Qual è il significato del teorema di Fermat nel contesto del libro?
- In che modo il libro affronta il concetto di numeri primi?
Il libro di Giorgio Tomaso Bagni mira a esplorare episodi storici e geografici della vita e delle ricerche di matematici del passato, offrendo spunti didattici attraverso brani antologici e attività di laboratorio.
Il libro tratta temi come la scoperta degli irrazionali, il paradosso di Achille e la tartaruga, i numeri primi, i misteri dello zero, le operazioni con numeri immaginari, la geometria analitica, e il teorema di Fermat.
La scoperta degli irrazionali è presentata attraverso la figura di Ippaso, evidenziando l'importanza di questo concetto nella storia della matematica.
Il teorema di Fermat è discusso come un esempio di un problema matematico complesso, la cui dimostrazione originale non è stata trovata, ma che è stato risolto da A. Wiles nel 1993.
Il libro affronta il concetto di numeri primi attraverso il crivello di Eratostene e la dimostrazione di Euclide sull'infinità dei numeri primi, fornendo un metodo per determinare i numeri primi fino a un numero assegnato.








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo