Meccanica: Valentina, 50,0 kg , sale col suo skateboard su una rampa con la velocità  iniziale di 3,90 m/s . L'altezza massima della rampa è 50,0 cm . Calcola:...

Calcolare energia cinetica ed energia potenziale gravitazionale di un corpo in movimento: uguaglianza lavoro-energia cinetica

_francesca.ricci
di _francesca.ricci
Ominide
2 min. di lettura
Vota

Concetti Chiave

  • Valentina's initial kinetic energy is calculated as 380 J using the formula k = 1/2 m v^2.
  • The gravitational potential energy at the top of the ramp is 245 J, calculated using U = mgh.
  • The work done by Valentina while going up the ramp is -245 J, as her potential energy increases.
  • The final kinetic energy at the ramp's exit is determined to be 135 J by accounting for the work done.
  • Valentina's velocity upon leaving the ramp is calculated to be 2.32 m/s using v = sqrt(2k/m).

Valentina,

[math]50,0 kg[/math]

, sale col suo skateboard su una rampa con la velocità iniziale di

[math]3,90 m/s[/math]

. L'altezza massima della rampa è

[math]50,0 cm[/math]

. Calcola:

  • L'energia cinetica all'imbocco della rampa;
  • L'energia potenziale gravitazionale (rispetto alla quota di base e con
    [math] g =9,8 m/s^2[/math]
    ) all'uscita della rampa;
  • l'energia cinetica all'uscita della rampa;
  • la velocità con cui esce dalla rampa.

esercizi_dimanica

Svolgimento (1)

L'energia cinetica è data dalla formula:

[math] k = 1/2 m v^2 [/math]

Sostituiamo i dati:

[math] k = 1/2 \cdot 50 kg \cdot (3,90 m/s)^2 = 380 J [/math]

Svolgimento (2)

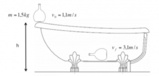
All'uscita della rampa, la ragazza si trova ad un'altezza di

[math]50,0 cm[/math]

, cioè di

[math]0,5 m[/math]

.

Calcoliamo la sua energia potenziale gravitazionale:

[math] U = mgh = 50 kg \cdot 9,8 m/s^2 \cdot 0,5 m = 245 J [/math]

Svolgimento (3)

All'uscita della rampa si avrà un'energia cinetica diversa da quella che si aveva all'entrata. Per calcolare questo nuovo valore, prendiamo in considerazione il lavoro esercitato dalla ragazza durante il tragitto. Sappiamo che:

[math] L = - ∆U = - (U_f - U_i) = U_i - U_f [/math]

All'inizio della rampa l'altezza alla quale si trova la ragazza è uguale a zero, quindi sarà nulla anche la sua energia potenziale. Avremmo quindi che:

[math] L = 0 - U_f = - U_f = - 245 J [/math]

Sappiamo inoltre che il lavoro è uguale alla variazione di energia cinetica, cioè:

[math] L = ∆k = k_f - k_i [/math]

Conoscendo il valore del lavoro e quello dell'energia cinetica iniziale, possiamo ricavare l'energia cinetica finale:

[math] L = k_f - k_i \to k_f = L + k_i [/math]

[math] k_f = - 245 J + 380 J [/math]

Svolgimento (4)

Dalla formula dell'energia cinetica, ricaviamo la velocità e determiniamo la velocità della ragazza all'uscita della rampa:

[math] k = 1/2 m v^2 \to v^2 = frac(2k)(m) \to v = \sqrt{frac(2k)(m)} [/math]

[math] v = \sqrt{frac(2k_f)(m)} = \sqrt(frac(2 \cdot 135J)(50,0 kg)) = 2,32 m/s [/math]

Domande da interrogazione

  1. Qual è l'energia cinetica di Valentina all'imbocco della rampa?

    2. L'energia cinetica all'imbocco della rampa è calcolata utilizzando la formula \( k = \frac{1}{2} m v^2 \), risultando in 380 J.

  2. Come si calcola l'energia potenziale gravitazionale all'uscita della rampa?

    3. L'energia potenziale gravitazionale all'uscita della rampa è calcolata con \( U = mgh \), risultando in 245 J, considerando un'altezza di 0,5 m.

  3. Qual è la velocità di Valentina all'uscita della rampa?

    4. La velocità di Valentina all'uscita della rampa è calcolata utilizzando la formula per l'energia cinetica, risultando in 2,32 m/s.

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Aiuto per Errori per Fisica
_francesca.ricci di Linustrike

aiuto studio
_francesca.ricci di Giorgia.obe

Esercizi con i vettori
_francesca.ricci di DAMIANO2011

I migliori insegnanti di Fisica

Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Matteo

Matteo S.

Supertutor
Verificato

Insegnante di Aiuto tesi, Algebra, Geometria, Matematica

a partire da 20 €/ora
most booked
Mostra altri Tutor